
Pellets of mass 2.0 g are fired in parallel paths with speeds of 120 m/s through a hole 3.0 mm in diameter. How far from the hole must you be to detect a 1.0-cm-diameter spread in the beam of pellets?
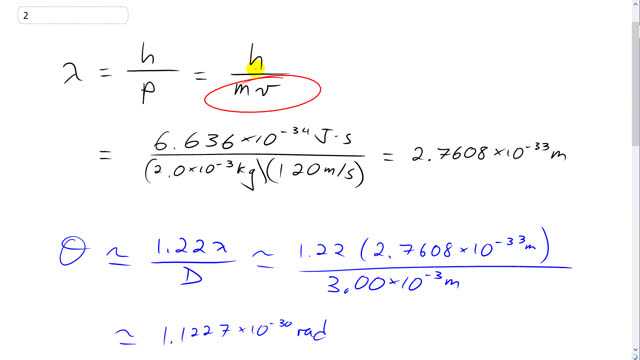
In order to watch this solution you need to have a subscription.
Hi! Just wondering when we can use the small angle approximation - you say here that it is when theta is less than zero, but how can that be?
Hi kbick, this is a good question since the small angle approximation is often a very useful trick to make the algebra much easier. Yes, I know it seems unbelievable that you can just replace with simply , so what you should do to convince yourself that it's acceptable when is small (I'm saying , but , or whatever variable represents the angle in your equation) is this: plot the graph of and on the same graph, but there's a catch. Zoom in on the graph so that you can only see between, say, -1 and 1. You'll notice the graphs look the same! This is the reason the approximation works, is that within this restricted domain of , both functions and give the same result. When you zoom out and look at larger values of , then of course the graphs do not look the same, and you can no longer claim that , like you can for small .
All the best,
Mr. Dychko