
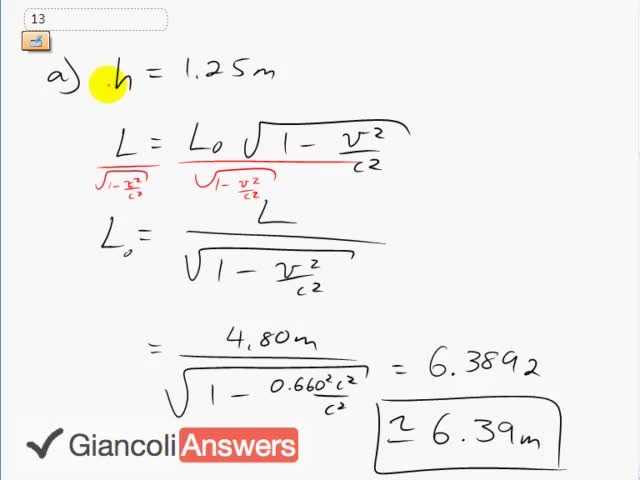
b)
c)
d)
In order to watch this solution you need to have a subscription.
Yes, explaining more on who sees proper time and who sees relativistic time would be great.
I don't understand part d. Why aren't we solving for t instead, to get an answer of 26.6 seconds? Shouldn't the time elapsed for the friend always be smaller than the time elapsed for us (the observer)?
Hi phamk, thanks for your question. Part d) could be phrased more explicity. The friend is now watching the Earth based observer zoom past, and is taking note of the time on the Earth observer's watch, which is at different locations between the start and end time. This means the friend is not measuring proper time since the starting event (the Earth base observer's watch at the initial time) is not in the same place as the ending event (the Earth based observer's watch at the end time).
The result of each person reporting the same time elapsed on the other person's watch when their own watch shows 20.0 s passed has some symmetry to it. We expect similar results from each perspective since no one perspective is special compared to the other.
Relativity is definitely confusing since it contradicts our slow moving day-to-day experience!
Hope this helps,
Mr. Dychko