
In order to watch this solution you need to have a subscription.
ok
Hi mattne, sorry for the late reply... summer holidays make things go a little slower...
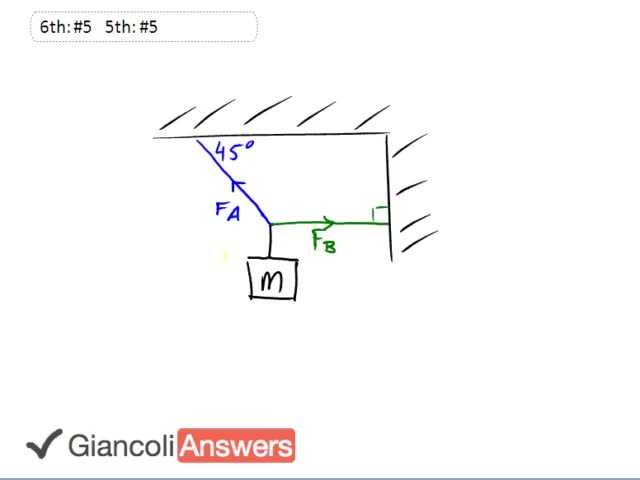
FB isn't related to an angle since it's straight horizontal, so there's no need to separate it into components. It's all in the x-direction. I can see where you're coming from though, since there's an equation that says . What this equation is saying is that the horizontal component of FA equals FB. The angle is related to FA, and it's used to find the horizontal component of FA. For equilibrium, all the horizontal components of all the forces have to be equal, but there's no trig. for FB since it's already horizontal.
Hope this helps, and good luck with your studies.
Why is sin used for FB? The picture just shows a straight line how do we relate the angle to FB?