
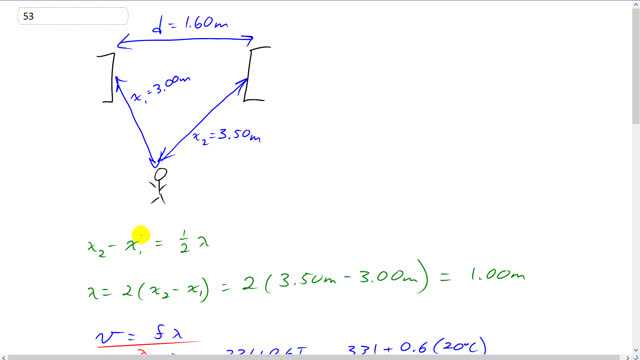
Two loudspeakers are 1.60 m apart. A person stands 3.00 m from one speaker and 3.50 m from the other.
- What is the lowest frequency at which destructive interference will occur at this point if the speakers are in phase?
- Calculate two other frequencies that also result in destructive interference at this point (give the next two highest). Let .
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We'll get destructive interference when the path length difference from one loudspeaker compared to the other is half a wavelength. And so in this x2 minus x1 equals half a wavelength, that'll be the first wavelength at which destructive interference will occur. So, we can multiply both sides by 2 to get λ and that works out to 2 times 3.5 minus 3 which is 1 meter. And then we figure out what frequency that wavelength corresponds to by dividing both sides of this formula by λ. And you get frequency is v over λ. And that's 331 plus 0.6 times 20 degrees Celsius divided by 1 meter. And that's 343 hertz. Now, in general, you'll get destructive interference when the path length difference equals half a wavelength plus any whole number times the wavelength. So, in part a, we assume that we have n is 0 in which case it's just worked out to 1/2 λ but you can also have n equal to 1 or n equal to 2 and so on. And then you get the next wavelength at which you'll have destructive interference there. So, at this at this single position, you can have destructive interference for many different specific wavelengths. According to this formula here. So, the next wavelength that'll destructively interfere will be x2 minus x1 equals 1/2 λ plus 1 times λ which is 3 over 2 λ and in which case λ is 2 times x2 minus x1 over 3 when you multiply this by 2 over 3 and then multiply this by 2 over 3. And so the frequency would be this wave speed, v, divided by λ which is the same as multiplying by its reciprocal so, that's why I have this multiplied by 3 over 2 times the difference in distances to the loudspeaker. And this works out to 1.0 times 10 to the 3 hertz. And there's two significant figures there because when you take this difference, 3.5 minus 3, it's going to be 0.50 meters. And 0.50 has two significant figures. And then after all this multiplying, it can have two significant figures in the answer. And then for n equal to 2 this is going to be 5 λ over 2 and in which case λ is 2 x2 minus x1 over 5. And then plugging that into the frequency formula gives 5 times 331 plus 0.6 times 20 degrees Celsius divided by 2 times the difference in path lengths which is 1,700 hertz.