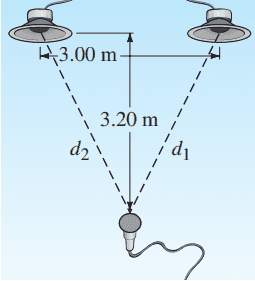
Two loudspeakers are placed 3.00 m apart, as shown in Fig. 12–37. They emit 474-Hz sounds, in phase. A microphone is placed 3.20 m distant from a point midway between the two speakers, where an intensity maximum is recorded.

VIDEO TRANSCRIPT

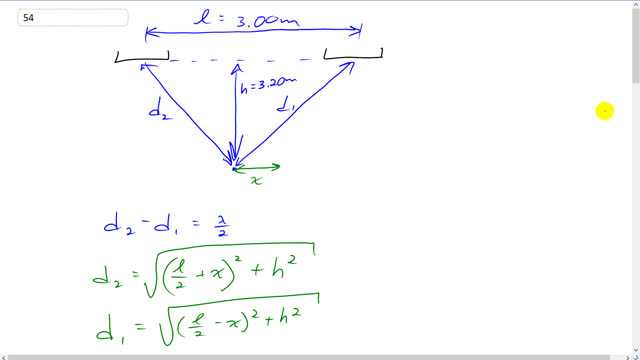
This is Giancoli Answers with Mr. Dychko. OK. You're gonna have to fasten your seat belt because there's a lot of algebra coming up here in order to answer this question. It sounds simple enough to answer but mathematics gets a little bit tedious shall we say. But it's a, you know, conceptually it's not too difficult to get. So, let's dive in here. You should have to be patient with the amount of work it's going to take. So, we're gonna have destructive interference when the path length difference between the point where the ear is and the distance to each of the loudspeakers when that difference between those distances is λ over to half a wavelength that's when you'll have your first point of destructive interference. So, when moving directly horizontally from this midpoint here. That's the midpoint between the two loudspeakers. After you make that movement, you're gonna have a distance, d2, to the left hand loudspeaker. This is no the new d2. That's going to be... l over 2. l is the distance between the loudspeakers. So, here's the midpoint, l over 2, plus an additional distance, x here, that's going to be one leg of this right triangle going to this new point here. And this distance here, and I guess you might call it the y direction. This distance I called h is still the same 3.2 meters. But to calculate d2 we're going to have to take this leg which is l over 2 plus x and square that. And then add to that h squared. And take the square root of it to find d2. And d1 will be the same sort of idea except now we're going to look at this thing here, that's the hypotenuse now. And one leg of the right triangle is here and that's going to be l over 2. Take away x, l over 2 minus x. And that's this distance here. And then this is still h. And so l over 2 minus x, all squared, plus h squared, all square rooted, gives d1. So, when d2 minus d1 is λ over 2 then we're going to have destructive interference. And so we need to solve for x such that that happens. So, here's a substitution into this formula from each of these lines. And we have d2 minus d1 equals λ over 2. So, we'll take this to the right hand side so that we don't have, it's messy to have two square roots on the same side of the equation when we square both sides. So, we'll have, take it to the right hand side and then we have this line here, I haven't done anything except move that to the right side which makes it plus. And now we're gonna square both sides to get rid of the square root sign or at least, you, know as much as we can although, because we're still gonna be left with the square root sign as it turns out but, but we have to start somewhere. So, we get to this line we'll square both sides which gives us l over 2 plus x squared plus h squared, and that's just the radicand. And that equals λ squared over 4. By the way it's good to just have this memorized a plus b squared is a squared plus 2 a b plus b squared so, when you square a binomial you have the first term squared plus 2 times the first times the second term plus the second term squared. And likewise if you have a difference in your binomial. So. If you have a minus b, it's exactly the same except you have a minus 2 a b for the cross term. So, that's a squared minus 2 a b plus b squared. Keep these two things in mind as we're going through all this stuff here. So, this is like the a and plus this is like the b. And so we have a squared is λ squared over 4 plus 2 times the first thing times the second thing. Well, 2 times λ over 2 is this λ. And then times the second thing which is square root of l over 2 minus x, all squared, plus A squared. And then plus this second thing squared which is itself the radicand, the thing under the square root sign written here. So, that's all over 2 minus x squared plus h squared. OK. And then, what did I do next? Yeah, I put the square root term on its own on one side of the equation. So, that we're gonna square both sides again. And then finally we'll be completely rid of any square roots because this thing is gonna be by itself is not going to be any binomial, there's not going to be any square root left in the cross term. And so then we'll be able to solve for x more easily that way. So, this whole thing is rewritten there unchanged. And we have this move to the left hand side, and in the process I squared it. So, I wrote a minus sign here because initially it's plus and then left everything inside according to this pattern here. So, we have l over 4 squared minus 2 times l over 2 minus x which is just minus lx, plus x squared. And then also take this to the left hand side as well. So, that's minus λ squared over 4. And that equals this thing on its own. And then when you distribute this negative into the brackets there, you'll end up with l squared over 4 minus l squared over 4 which cancels to make 0. You have lx minus negative l x which is lx plus lx and so it's 2 lx. And then you'll have x squared minus x squared which makes 0. And so we're left only with only with 2 lx minus the λ squared over 4 on the left side, and the right side I've written again unchanged. So, now we've got things looking as simple as they can be and we'll square both sides again. And on the right hand side you have λ squared times the radicand here. So, that's l over 2 minus x squared plus h squared. And on the left side we're applying this a squared minus b, or, sorry, a minus b, all squared pattern, squaring a binomial. And you have the first thing squared, that's 4 l squared x squared minus 2 times the first thing time the second thing. So, that's gonna work out to 4 lx minus λ squared over 4. So, the 4 is cancel and we're left with lx λ squared. And then plus the second thing squared, so, that's λ to the power of 4 over 16. And that equals λ squared times the radicand, yeah. And then just repeating the left hand side a couple of times here as I do a bit of work in the right hand side. And squaring this binomial gives l squared over 4 minus lx plus x squared. And then after doing that, multiply by the λ squared out here. And you end up with this. And then also I'll multiply the λ squared by the h squared to get this. And then multiply entirely through by the λ squared to get λ squared l squared over 4 minus l x λ squared plus x squared λ squared plus λ squared h squared. Then move everything onto the same side of the equation so that it's easier to see what cancels with what. And we have... I'm writing terms with equal powers of x beside each other. So, we have this 4 l squared x squared. This really is a bookkeeping issue here now. You have to make sure your minus signs are correct and you're collecting terms that actually are like. And when you say like terms, it means terms with the same powers of x. So, we have 4 l squared x squared, copied. And then the x squared term on the right hand side is this one so, let's write that right beside it. And so when we take it to the left side it's going to be minus. So, minus x squared λ squared. And then we'll have let's get rid of this. All these yellow highlights are a bit of a distraction now. Bit of noise. OK. So, we have the x squared terms taken care of. Let's cross them up. Done. Taking care of that. And then we want to take terms containing x to the power of 1. So, that's this one copied that's taken care of. And then on the right hand side we have... We have this term which we'll take to the left side making it plus, and so there it is. It turns out that these cancel anyway. You know, maybe instead of crossing them out I should just check them off to say that they're taken care of. So, check, check, check and check. And then we have this λ to the power 4 over 16 written here. And then, well, there's nothing much else that's fancy to do, just bring these terms to the left hand side changing their signs. And there we go. Then I'm gonna have the letter x in them. So, we just move them over. Those are all constant terms. And an equal 0 on the right hand side. So, we should make sure that we have all the terms that we expect. We expect to have 1, 2, 3, 4, 5, 6, 7 terms. And sure enough we have 1, 2, 3, 4, 5, 6, 7 terms. So, our bookkeeping is looking good. And now collect them. So, these two things have the same factors but opposite signs, so they cancel. And we can factor out the x squared here, leaving us with x squared times 4 l squared minus λ squared and that equals λ squared times l squared over 4 plus h squared minus λ squared over 16. I did two things at once there first of all I factored out λ squared from each of these and then secondly I moved everything to the right hand side again. So, all their signs are opposite to what you see here. So, the l squared over 4 term became positive. The h squared term became positive as well. And this λ squared over 16 term which turns into λ or λ to the power 4 over 16 term became minus, λ to the power of 4 was 16 although you see λ squared here because I factored out λ squared. Then divide both sides by this bracket, take the square root of both sides and we finally have a formula for x. Well, that was a lot of work. So, if you made it this far, congratulations on your perseverance. So, when you divide all this right hand side by this, you'll end up with λ squared times some stuff, a fraction. And when you take the square root of both sides, the λ squared becomes λ. And but everything else has to stay under the square root sign. So, we have λ times square root of l squared over 4 plus h squared minus λ squared over 16 all divided by 4 l squared minus λ squared. I bet that was more complicated than you expected. And but there we go. That's what it is. Let's figure out λ. Speed of sound is frequency times wavelength. And you can find λ by dividing both sides by f, and we get 343 meters per second divided by 474 hertz which frequency of both loudspeakers. And that's 0.72363 meters. And so we'll substitute that in. So, we have 0.72363 meters times square root of the separation between the loudspeakers, that's l squared over 4 plus the y distance away from the loudspeakers vertically downwards. And that's 3.2 meters squared. There's a minus here not a plus. Minus 0.72363 meters over 16 squared and the top squared. And then divided by 4 times 3 meters squared minus 0.72363 meters squared, square root all at business. And you get 0.429 meters is the distance to the first position of destructive interference, and that's on either side of the midpoint. I wrote t on the right hand side but equally that same distance to the left would also have a position of destructive interference. Now, if the speakers are exactly out of phase that mean constructive interference will occur when you have distances that are, when the difference in distances to the loudspeakers is half a wavelength. And so we just figured out what that exposition is. And so instead of corresponding to destructive interference, it now corresponds to constructive interference. So, you'll have maxima at x is plus or minus 0.429 meters. And likewise with the minima, the destructive interference, that'll now occur where there was once before constructive interference. So, you'll have destructive interference at any path length difference equal to a whole number multiples of the wavelength. So, such as 0 for example. If you have these things exactly out of phase, a point that's equidistant between the loudspeakers, would have destructive interference.