
A two-component model used to determine percent body fat in a human body assumes that a fraction of the body’s total mass is composed of fat with a density of , and that the remaining mass of the body is composed of fat-free tissue with a density of . If the specific gravity of the entire body’s density is , show that the percent body fat is given by .
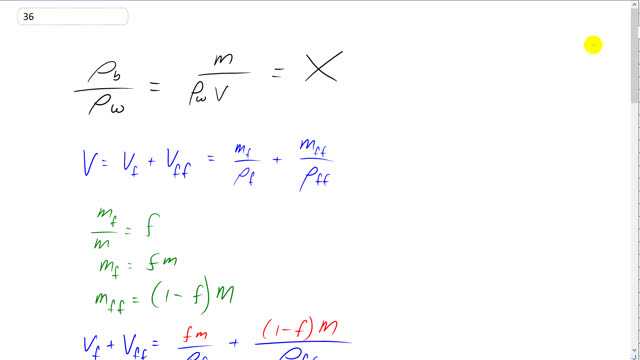
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. So this question involves a lot of algebra so fasten your seat belt as we wend our way through all that stuff there but hopefully I'll make it make sense. So we have the specific gravity of the body, it's the body's density divided by density of water, that's the definition of specific gravity; so we take that total mass of the body and divide by the total volume to get the density of the body and then divide that by density of water so this is specific gravity here as well and we are told that that equals the letter X. So we need some way to get this little f involved here because our final answer has to be to show that you know, f times a 100 which will be percent body mass equals some stuff that we are showing there— 495 over X minus 450. So this f has to be involved here somehow so we are gonna make it appear within this volume part. So we know volume is the volume of the fat in the body plus the volume of the fat-free part of the body and the volume of the body consisting of fat is the mass that is fat divided by the density of fat plus the mass that is fat free divided by the density that is fat free. Substituting you know, you have the density definition is mass over volume and you can solve for volume by multiplying both sides by V and dividing both sides by ρ and you end up with V on the left equals mass divided by density. So that's what I'm substituting here: mass divided by density in place of volume. And then further we can say that m f divided by m is f because f represents the fraction of the total mass which is fat so the mass that is fat divided by total mass is f and we can rearrange this by multiplying both sides by total mass and we get mass of the body which is fat is this fraction that is fat times the total mass and we are gonna substitute that in for m f here—that's what I did in that line— and then mass that is fat-free has to be 1 minus the fraction that contains fat times the total mass. I guess to explain that I would say m f divided by m plus m ff or m has to equal 1 because this makes up a 100 percent of all mass in the body so m ff has to equal 1 minus m f over m all multiplied by m but this thing right in here is f and so we have 1 minus f times m is m ff as shown here. Okay. So plug each of these things into these numerator's in this volume expression and we have the total volume that consist of fat plus volume that is fat-free is f times m over density of fat plus 1 minus f times m over the density of the fat-free material and then plugging that all in for total volume in this expression I guess this part of it anyway plugging in for V there in red I have total mass divided by density of water times this whole business for the total volume equals x and now... (what do I say here?) We want to solve for f which is a nasty thing because it's buried within this denominator and well, first of all, let's say multiply both sides by 1 over X and then that gets rid of the X on the right side and leaves us with an X on the left side so we have m over X and then multiply both sides also by this denominator so that on the left side, it disappears and on the right side, it's the only thing that's there because X over X makes 1 and then we are left only with 1 times this denominator and then switch the sides around too so that we have this unknown stuff on the left. So we have m over X equals this whole denominator and then I expanded the denominator too so I multiplied this ρ w into each of the terms so we have ρ w times f times m over ρ f plus 1 minus f times ρ w times m over ρ ff equals m over X. That might be the hardest algebra step in this sequence because I kinda did a couple things at once there but hopefully that made sense. Some teachers refer to what I did here as cross-multiplying; you can multiply... even that's not a very good way to explain it never mind the cross-multiplying. So.. there. Let's go to the next line! Let's expand this stuff and multiply both these terms in this bracket by ρ w times m so we have 1 times ρ w times m over ρ ff and by the way, the m's canceled... (okay there we go) so there's no m it's a common factor on both sides so we can divide both sides by it and it's gone so we have ρ w times 1 over ρ ff so that's just ρ w over ρ ff minus f times ρ w over ρ ff and I'm writing them as separate terms here and never mind keeping them as one fraction, make them two fractions because we wanna collect the two terms that contain the f. So we do that in the next line and we have f times ρ w being a common factor for both these terms and multiplied by, you know, what ends up being a 1 here over ρ f minus 1 over ρ ff and then this term got moved to the right hand side by subtracting it from both sides so it's ρ w over ρ ff. And then write this as a single fraction so common denominator makes this ρ ff over ρ ff, multiply this by ρ f over ρ f and you have ρ ff minus ρ f over ρ f times ρ ff. That's all I did in that line and then multiply both sides by ρ f times ρ ff so we have ρ f times ρ ff over X and then it's just the ρ f when you multiply this term by that denominator because the ρ ff's cancel and so you are just left with ρ f and then we are also dividing both sides by ρ w times bracket ρ ff minus ρ f and so that's where this comes from that's just, you know, copied there but whereas over here, it's missing the ρ w because it cancels with this one and so it's just ρ ff minus ρ f. And finally, we plug in some numbers and it all handily works out to what we needed to. So we have density of fat is 0.90 grams per centimeter cubed times 1.10 grams per centimeter cubed for the fat-free material divided by X times 1 gram per centimeter cubed—density of water— times a difference between those fat free and the fat density minus 0.90 divided by 1.10 minus 0.90 and you end up with 4.95 over X minus 4.5 that's the fraction which is fat and if we want the percent, we have to multiply both sides by 100 and so this gives a percent which is body fat which will be 495 over X minus 450.