
Giancoli's Physics: Principles with Applications, 7th Edition
24
The Wave Nature of Light
Change chapter24-3: Double-Slit Interference
24-4: Visible Spectrum; Dispersion
24-5: Single-Slit Diffraction
24-6 and 24-7: Diffraction Gratings
24-8: Thin-Film Interference
24-9: Michelson Interferometer
24-10: Polarization
Question by Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014, Reprinted by permission of Pearson Education Inc., New York.
Problem 11
Q
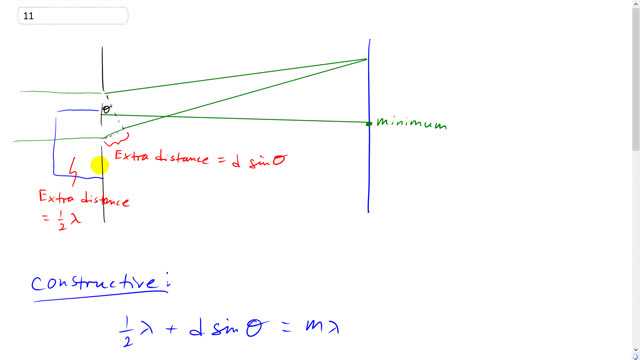
Suppose a thin piece of glass is placed in front of the lower slit in Fig. 24–7 so that the two waves enter the slits out of phase (Fig. 24–58). Draw in detail the interference pattern seen on the screen.
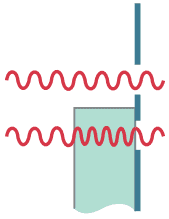
Figure 24-58.
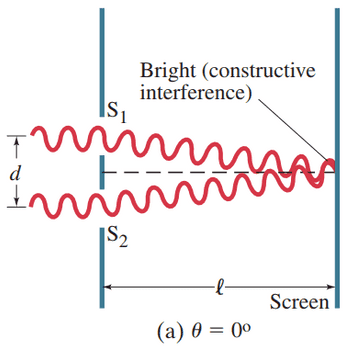
Figure 24-7 How the wave theory explains the pattern of lines seen in the double-slit experiment. (a) At the center of the screen, waves from each slit travel the same distance and are in phase. [Assume .]
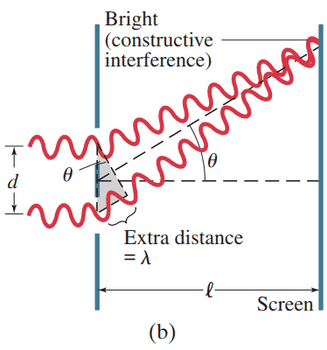
Figure 24-7 How the wave theory explains the pattern of lines seen in the double-slit experiment. (b) At this angle , the lower wave travels an extra distance of one whole wavelength, and the waves are in phase; note from the shaded triangle that the path difference equals .
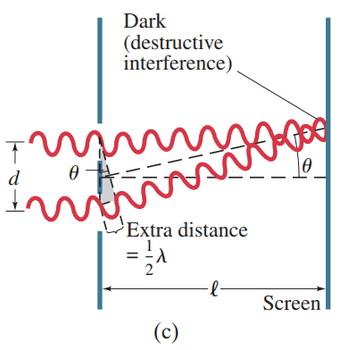
Figure 24-7 How the wave theory explains the pattern of lines seen in the double-slit experiment. (c) For this angle , the lower wave travels an extra distance equal to one-half wavelength, so the two waves arrive at the screen fully out of phase.
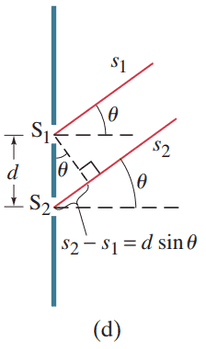
Figure 24-7 How the wave theory explains the pattern of lines seen in the double-slit experiment. (d) A more detailed diagram showing the geometry for parts (b) and (c).
A
constructive:
destructive:
The interference pattern is reversed.
destructive:
The interference pattern is reversed.
In order to watch this solution you need to have a subscription.
Giancoli Answers, including solutions and videos, is copyright © 2009-2025 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.