
How thick (minimum) should the air layer be between two flat glass surfaces if the glass is to appear bright when 450-nm light is incident normally? What if the glass is to appear dark?
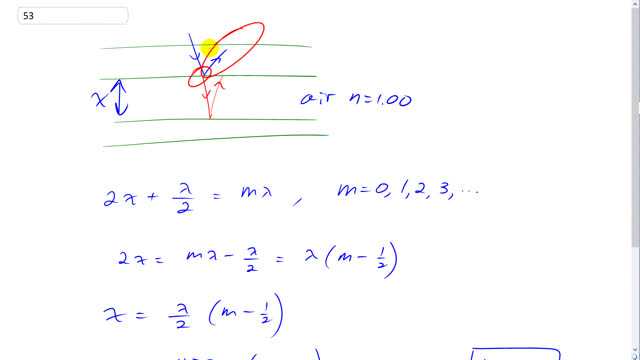
In order to watch this solution you need to have a subscription.
Hello,
there is a second question in this problem: "What if the glass is to appear dark?"
I am curious to see that solution.
thanks,
Spanda
Hi spanda2u, well, in a pinch I can give a written solution: the minimum separation would be zero, or if you want a non-zero answer then the first separation for destructive interference would be ( with sig. figs. considered). It's important to know why "zero" creates destructive interference ("zero" isn't really zero, but rather a microscopic separation in which a very tiny air gap still exists despite the two pieces of glass touching). At "zero" separation, the ray reflecting from the bottom piece of glass undergoes a phase shift since it's initially in a medium of low index of refraction (a microscopic layer of air) and then reflecting off a medium of high index of refraction (bottom piece of glass). This business about a ray undergoing phase shift when reflecting from a medium of higher index of refraction that the medium in which it is initially is just a rule that has to be memorized. Since the ray reflected from the bottom piece of glass is shifted , whereas the ray reflected from the bottom of the top piece of glass is not phase shifted at all (since it's initially in a high index medium, glass, reflecting off a low index medium of air), and there is no additional path length travelled by the bottom ray (or a negligible path length to be precise), these two rays are out of phase with respect to each other and so they destructively interfere (dark!). The next dark separation would occur when the separation between the pieces of glass results in an additional path length travelled by the bottom ray to be . The bottom ray travels the separation twice (once down, then again back up), so the separation that causes an additional path length of is . This makes the first non-zero dark separation equal to .
Hope that helps,
Mr. Dychko
Thank you.