
In Fig. 4–56 the coefficient of static friction between mass and the table is 0.40, whereas the coefficient of kinetic friction is 0.20.
- What minimum value of will keep the system from starting to move?
- What value(s) of will keep the system moving at constant speed? [Ignore masses of the cord and the (frictionless) pulley.]
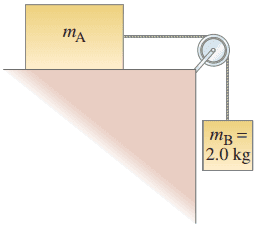
In order to watch this solution you need to have a subscription.
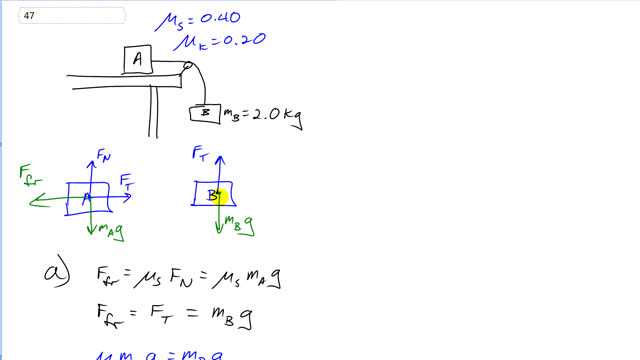
This is Giancoli Answers with Mr. Dychko. We have this system which is at rest for part A and when we consider block B, since it's at rest, the tension force upwards is going to be equal to the gravity downwards because there's no acceleration and so, this tension force that's being exerted upwards on block B it's the same tension throughout this string. And so, it's the same tension force that's being exerted to the right on block A. And since it's at rest that means the friction force to the left has to be equal to the tension force. And so... And that's what we say here, the friction force equals the tension force. And the tension force is mB times g and the friction force also we know is coefficient of static friction times the normal force on block A. And the normal force on block A is the weight of block A because there's only one force upwards and that's the normal force, then it has to equal the total forces down which in this case is just gravity. And so, it's normal forces mA g. And so, since each of these equals the friction force, we can say that they are equal to each other. And then we can divide by muS g, and the g's cancel. And we're left with the mass A at a minimum is going to be mass B divided by the coefficient of static friction. So, 2 kilograms divided by 0.4 which is 5 kilograms. And in part B it's actually very similar because there's still no acceleration in the system when it's moving at constant speed. And so, when it's moving at constant speed the tension force is still equal to the weight of block B because there's no acceleration. And the only difference now is that the friction to the left on this block A is now going to be given by coefficient of kinetic friction times, mA g. And we can still say, though, that this coefficient of kinetic friction times mA g is still equal to mB g since mB g is the weight of block B in it, it is the tension force which is acting to the right on block A. And divide both sides by muK g. And you get the mass A for the case of constant speed during, while it's moving is gonna be 2 kilograms times 0.2 which is a coefficient of kinetic friction which is 10 kilograms, and I wrote it in scientific notation just to be clear that there are two significant figures in the answer. So, that's 1.0 times 10 to the 1 kilograms.
I don't understand, conceptually, how a 2kg box can not move pulling a 5kg box but move it at constant speed pulling a heavier box. Can you please clarify this? Thank you.
Hi Nategrana, thanks for the question. The difference between the scenarios has to do with static friction vs kinetic friction. The main idea to consider in both parts is that the more massive the box on the table, the harder it is to pull it since it will be pressed up upon more strongly by the surface (aka. the Normal force) and thereby experience more friction. Our goal is to find the maximum mass possible before that friction prevents acceleration. Notice that I mention "prevents acceleration", since being at rest or moving at constant speed are both examples of not accelerating, and in either case the friction is fully equivalent in magnitude to the tension resulting from the hanging mass.
The mass of the box on the table is only one part of the issue, and the other part is the coefficient of friction. The higher the coefficient of friction, the more friction force results from a given mass. So, in part a) we're dealing with the box on the table at rest, and this means the coefficient of friction to use is the coefficient of static friction. In part b) since the box is sliding, we use the coefficient of kinetic friction. The coefficient of kinetic friction is always lower than the coefficient of static friction. This means that for the force of friction to equal the tension force, the case b) with a smaller coefficient of friction calls for greater mass than compared to the case of part a) where a higher coefficient of static friction means a lower mass is needed to equal that same tension force.
Hope that helps,
Mr. Dychko
I would like for you to explain the whole process. Why did you use this friction formula. How did you get the friction formula to calculate the mass?