
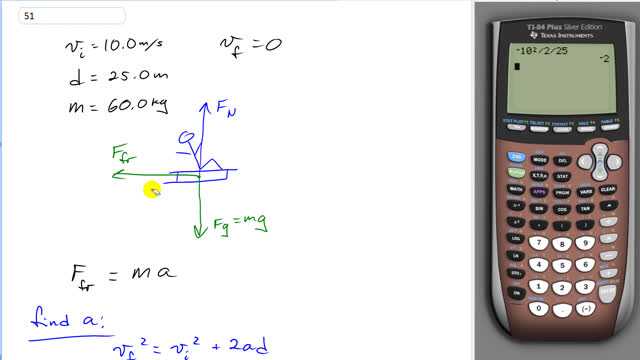
A child on a sled reaches the bottom of a hill with a velocity of 10.0 m/s and travels 25.0 m along a horizontal straightaway to a stop. If the child and sled together have a mass of 60.0 kg, what is the average retarding force on the sled on the horizontal straightaway?
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. When this child on a sled reaches the bottom of the hill, they have an initial speed of 10 meters per second. And the retarding force is due to friction and so, that's what I've drawn here on this free body diagram, and there's also normal force up and gravity down although it turns out those won't be relevant for this calculation here. Final velocity is zero and the child travels a distance of 25 meters, they have a mass of 60 kilograms. So, the friction force is the only force horizontally and so, that makes it the net force. And net force always is mass times acceleration. So, we'll have to find the acceleration first using kinematics and then multiply by the mass to get our answer for the friction force. So, final velocity squared equals initial velocity squared plus 2ad and V initial, or sorry, V final is zero, so, get rid of that term. And then we'll subtract Vi squared from both sides and then divide both sides by 2d to solve for a. And we have acceleration is negative initial velocity squared divided by 2d. So, it's negative 10 meters per second squared divided by 2 times 25. And it gives negative 2.00 meters per second squared. And the retarding force then is mass times acceleration, 60 kilograms times negative 2 which gives negative of 1.20 times 10 to the 2 kilograms. And I wrote it in scientific notation instead of writing 120 because writing it this way is ambiguous as to how many significant figures are suggested, strictly speaking there's only two. And so, since we should have three I wrote it this way. And the negative sign means that this force is in the opposite direction to the initial velocity. And with the initial velocity being positive, that means this has to be negative.
Hey Mr. Giancoli,
Thank you so much for your videos! They are really helpful! Just so you know, this problem asked for the retarding force so the units should be Newtons, not kilograms.
Hi sueqrahn, thanks for noticing that typo. You're quite right that it should be written as Newtons and not kilograms.
Keep up the good work,
Mr. Dychko
In this problem, can I use the formula, Ffr = μk*Fn? I calculated μk to be .2. So the answer should be .2*60kg*9.8m/s2 = 117.6N. Is this just another way of solving the problem or did I get it wrong? Thank you!!
Hi theovilous, thanks for the question. While is a correct formula, I'm not sure how you calculated ? It doesn't look possible with the information given, so I think using acceleration is the only method available for solve this one.
All the best,
Mr. Dychko
I considered retarding force as friction. So I set the formula Ffr = ma --> μkmg=ma --> μk = a/g --> μk = 2/9.8 = .2.
So based on the formula, Ffr=μkFn, Ffr=μkmg = .2 * 60kg * 9.8m/s2 = 117.6N.
Does this approach work as well? my result is very close to your answer which is 120N.
Thank you for your quick response! I am learning a lot from you!
Hi theovilous, ah, now I understand your approach. Yes, you can do what you're suggesting. I suspect that if you keep lots of digits in your answer for (to avoid intermediate rounding error), that your answer will match the answer here exactly to three significant figures. The approach you're suggesting takes more steps, but it's perfectly valid.
I'm glad you're enjoying the solutions!
All the best,
Mr. Dychko