The coefficient of kinetic friction for a 22-kg bobsled on a track is 0.10. What force is required to push it down along a $6.0 ^\circ$ incline and achieve a speed of 60 km/h at the end of 75 m?

VIDEO TRANSCRIPT

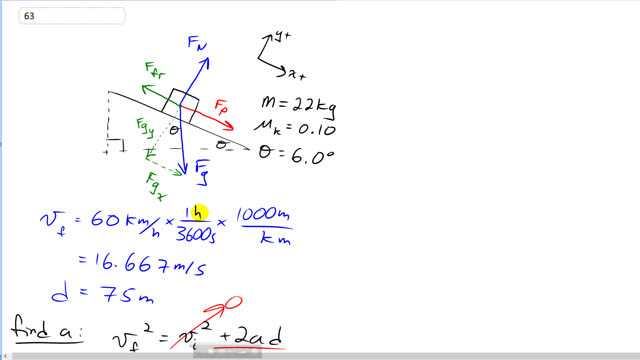
This is Giancoli Answers with Mr. Dychko. By the time this bobsled gets to the end of 75 meters, we want it to have a speed of 60 kilometers an hour but we'll change that in to meters per second by multiplying by one hour for every 3600 seconds and then times by 1000 meters for every kilometer, and we get meters per second and that's 16.667 meters per second final speed. So, here's the free body diagram showing this force that's pushing it along down the ramp. There's friction moving against the velocity. Velocity is down the ramp. So, kinetic friction is always opposite the direction of velocity, and so, it's up the ramp. And we have gravity helping out, getting it down the ramp as well some component of it anyhow. Coefficient of kinetic friction is 0.1 this is slope as an angle of six degrees, and the mass of the Bob's, that's 22 kilograms. And we'll need to figure out what acceleration is needed in order for it to reach this final speed after this certain distance. And then knowing that acceleration which is what we got here, we'll have Newton's second law with all these forces equaling mass times that acceleration and then figure out what FP should be because we know what the friction and the x component of gravity are. So, first what's the acceleration required. So, final velocity squared equals initial velocity squared plus 2ad. And it starts from rest, so, this term disappears. And then divide both sides by 2d. And we get acceleration is final velocity squared over 2 times displacement. So, that's 16.667 meters per second squared divided by 2 times 75 meters which is 1.8519 meters per second squared acceleration. And that's what will go here for a and we can see from this diagram, we have FP and Fgx, both in the positive x direction. And so, we have those added together and then minus the force of friction going in the negative x direction. And that all equals mass times acceleration because this is the net force. And Fgx is mg sine theta because it's the opposite leg of this triangle here. So, sine theta, and so, it's sine times mg. And then force of friction is muK times FN. And since there's no acceleration perpendicular to the ramp the normal force has to equal the force going in the other direction perpendicular which is only Fgy and Fgy is mg times cos theta because this is the adjacent side, adjacent to this angle theta. And we'll make substitutions then. We'll also isolate this FPE by moving this friction force to the right which makes it positive and move this Fgx to the right which puts a minus in front of it as shown here. And we'll make substitutions now, for F, force of friction in Fgx. So, force of friction is muK mg cos theta. And Fgx is... Fgx x is mg sine theta. So, that's what we write here. And so, we have the force required to push it down is ma plus muK mg cos theta minus mg sine theta. m is the common factor, we'll factor that out. And so, we have m times bracket acceleration plus coefficient of kinetic friction times g times cos theta minus and g times sine theta. So, 22 kilograms times 1.8519 meters per second squared acceleration that we calculated earlier here. And then plus 0.1 times 9.8 meters per second squared times cos of six degrees minus 9.8 meters per second squared times sine of 6 degrees which is 40 newtons. That's the force that has to be applied the whole time along the 75 meters in order to get this bobsled up to a speed of 60 kilometers an hour after 75 meters