
Uphill escape ramps are sometimes provided to the side of steep downhill highways for trucks with overheated brakes. For a simple upward ramp, what minimum length would be needed for a runaway truck traveling 140 km/h? Note the large size of your calculated length. (If sand is used for the bed of the ramp, its length can be reduced by a factor of about 2.)
In order to watch this solution you need to have a subscription.
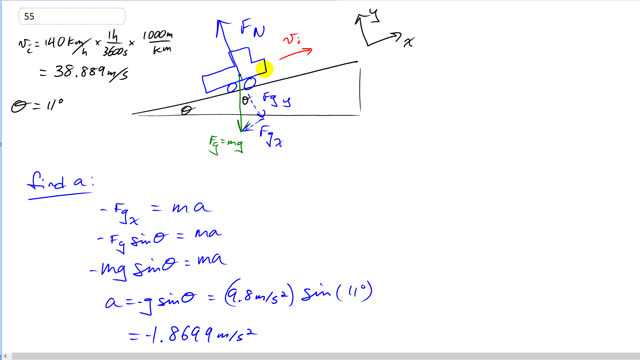
This is Giancoli Answers with Mr. Dychko. We're considering a friction free case, where the only thing slowing the truck down as it goes up this safety ramp is the component of gravity that's down along the ramp. So, the initial speed of the truck is 140 kilometers per hour but we'll convert that to meters per second by multiplying by 1,000 meters per kilometer, and by one hour for every 3,600 seconds, giving us meters per second. And that's the same as dividing by 3.6. So, we get 38.889 meters per second is the initial velocity. And we'll take positive to be up the ramp. The ramp is inclined at 11 degrees. And the first step is to find acceleration knowing something about the forces. And then after we find that acceleration and knowing the initial speed we can figure out what distance it'll have to travel before it comes to a stop. So, force of gravity in the x direction is in the negative direction. And so we put negative Fgx equals ma because this is the only force in the x direction, so, that makes it the net force, and that makes it equal to ma, Newton's second law. And this is the opposite leg of this gravity force triangle. And so, that means we use sine theta to calculate this opposite component. And so, we have Fg sine theta equals ma. And Fg is mg. So, we have negative mg sine theta equals ma, and the m's cancel. And we'll solve for a and it's just a equals negative g sine theta so, it's 9.8 meters per second squared times sine of 11 which is negative 1.8699 meters per second squared acceleration. Then it becomes a kinematics equation or question. So, we have final velocity is zero, comes to a stop. And we'll subtract V initial squared from both sides. And we have 2ad equals negative V initial squared, divide both sides by 2a to figure out the distance traveled. So, the distance will be negative of V initial squared over 2a so, it's negative of 38.889 meters per second, square that, divided by two, times 1.8699 meters per second squared and we get a distance travel of 4.0 times 10 to the 2 meters. I could have written 400 meters but it would be unclear how many significant figures it has, one technically. So, since there should be two, we have 4.0 times 10 to the 2 meters. And that's a long way. So, you can see that the textbook suggestion of using sand in order to introduce significant amount of friction here. So, force of friction along the ramp downwards wouldn't be a really good idea.
How do we know that it is a frictionless ramp? Is it because the question does not give us the coefficient of friction so we assume that it is frictionless?
Hi chaegyunkang, thanks for the question. Since the question has a truck driving on the ramp, we assume there is only rolling friction, which we assume is negligibly small. There is no sliding, so there's no kinetic friction. While there is static friction, since we assume the brakes are not being applied (since the ramp is used when the brakes have failed), this means the tire is not applying a horizontal force due to static friction, and so the pavement is not in turn applying a Newton's 3rd law reaction force on the truck. In other words, static friction is not slowing down the truck. There is only rolling friction, which we can ignore.
Hope this helps,
Mr. Dychko