
A car can decelerate at without skidding when coming to rest on a level road. What would its deceleration be if the road is inclined at and the car moves uphill? Assume the same static friction coefficient.
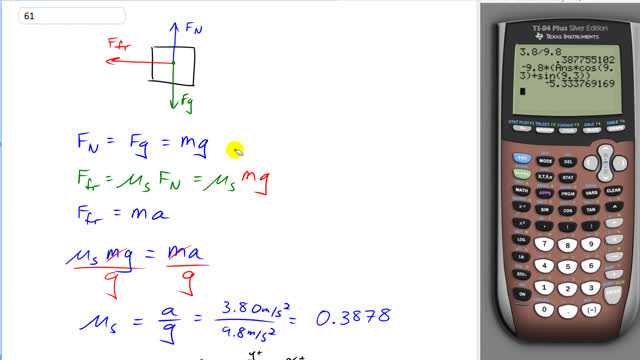
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. So, we use information about how the car travels on a level road to figure out the coefficient of static friction. And then after we know that, we'll be able to answer the question about when it's on an incline. So, here's the free body diagram of the car, on the flat. So, we have normal for straight up and gravity down and friction to the left, assuming that its velocity is initially to the right. And so, the normal force is equal to gravity since there's no vertical acceleration. The up force has to equal the down force and gravity is mg and so, then when we have friction force equals muS times FN, we can plug in mg instead. And so, we have muS times mg. Coefficient of static friction times gravity is the friction. The friction force also is the only force horizontally and so that makes it the net force. And so, by Newton’s second law, it's equal to mass times acceleration. And since this equals friction and this equals friction, we can equate them together. So, we have muS mg equals ma, cancel the m's, divide both sides by g, and we get the coefficient of static friction is a over g, 3.8 meters per second squared divided by 9.8 and we have 0.3878 coefficient of static friction. And that's a useful number that we'll use in a minute. Now, when the car is on an inclined road, inclined at 9.3 degrees and with a velocity initially upwards, the question is, what will the deceleration in the car be? We have positive x direction up the ramp, say, and we have friction acting against that velocity as kinetic friction always does. And so if friction is going down the ramp and it's going down the ramp together with the x component of gravity also going down the ramp, both of them are in the negative direction. And they both make the net force in the x axis. And so, that makes it equal to ma now, the friction force is muS FN. And FN since there's no acceleration perpendicular to the ramp, has to be equal to the y component of gravity which will find by going gravity times cos theta. Cos theta since this y component is the adjacent leg of this gravity triangle. And friction force, you know, and then we can plug in mg for Fg and we get this line here. So, let's plug that in for friction, muS mg cos theta minus the x component of gravity which is the opposite leg of this gravity triangle. So, that makes it mg sine theta and then that equals ma. So, I've substituted into that Newton's second law to get this line here, that's equation 1b. And then we'll solve this for a by dividing both sides by m. And we get a is negative g times coefficient of static friction times cos theta plus sine theta. So, I factored the negative g out of both terms just because that looks a little more clean. So, we have negative 9.8 meters per second squared times 0.3878 times cos 9.3 plus sign of 9.3, gives negative 5.3 meters per second squared will be the acceleration of the car. And the negative means that it's going in, acceleration is directed in the negative direction against the velocity. So, you might call it a deceleration of 5.3 meters per second squared.
If the car was skidding what difference would it make to the problem? Does it change to kinetic friction when it starts to skid?
Hi chaegyunkang, it's always true that kinetic friction is less than static friction, all else being equal. In this question, however, it doesn't really matter what type of friction is mentioned, since we're not given the coefficient anyway. What matters is the deceleration the car, from which we calculate the coefficient. Be it a static or kinetic coefficient is not important. The important thing is that the type of friction on the incline is the same type of friction on the level surface so that we can be sure that whatever we calculated on the level surface will still apply on the incline.
All the best,
Mr. Dychko