VIDEO TRANSCRIPT

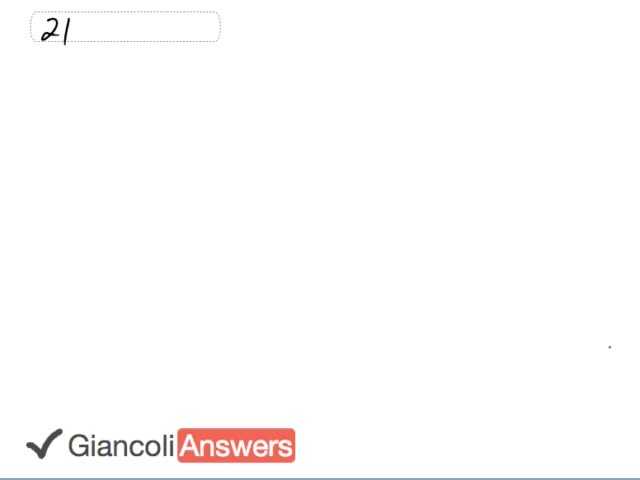
We’re going to start by considering the seventy five kilometer per hour car, it goes around the banked curve; it is perfectly banked meaning that there is no friction needed. So in our first case our picture will look like this. We have a banked curve, we don’t know the banking angle and that would be the whole point to this part of the question actually, we’re going to find out that banking angle theta. And we have a normal force going perpendicular to the road surface, and we have gravity going straight down. Normal force has components, that’s the Y component straight up and the X component straight to the left and our co-ordinate system has X straight to the left and Y is going up. So this X axis is not going along the ramp, instead its pointing straight to the left, to the center of the circle that car is travelling in. We’re going to start by saying that ‘FNy’ equals ‘Fg’, and ‘FNy’ is the adjacent component of this right triangle, and here’s theta, so ‘FNy’ is the adjacent component to theta. So we have ‘FN’ cosine theta equals ’m’ times ‘g’ substituting for gravity. The normal force is ’m’ times ‘g’ over cosine theta. We know the X component of the normal force is the opposite leg to theta so its ‘FN’ sine theta and we can make a substitution for ‘FN’: ’m’ times ‘g’ sine theta over cosine theta which is 'm’ times ‘g’ tangent theta. You have to know the trigonometric identity which says sine theta divided by cosine theta is tangent theta, that’s always true. Now ‘FNx’ also is the centripetal force because there is no friction so this is the only thing pointing towards the center of the circle. This ‘FNx’ is entirely responsible for the centripetal force so its ’m’ times ‘v’ squared over ‘r’. So now we can say that this equals ’m’ times ‘g’ tangent theta, and then we’ll solve for theta. So we have: ’m’ times ‘g’ tangent theta equals ’m’ times ‘v’ squared over ‘r’. Cancelling the ‘m’s’, divide both sides by ‘g’ and we’ll get tangent theta is ‘v’ squared over 'r' times ‘g’ which means that theta is the inverse tangent of twenty point eight three meters per second squared divided by eighty eight meters and also divided by nine point eight, this makes twenty six point seven zero seven eight degrees. And I should explain where this twenty point eight three came from: that’s seventy five kilometers per hour divided by three point six gives you twenty point eight three. Three point six is a conversion factor from kilometers per hour to meters per second. We know the angle now and that’s going to help us in part b when we figure out what is the coefficient of friction needed so that the car can go ninety five kilometers per hour. So now we’re going to consider ninety five kilometers per hour which divided by three point six makes twenty six point three nine meters per second. In the Y direction, you know we really should get another picture here to really understand how to write that equation for the Y direction. So we have the car here again. Normal force, gravity, Y component for normal force, ‘FNy’, X component for normal force, I’m just going to label that ‘FN’, label this one ‘Fg’ and we have friction going down the ramp because it opposes motion so its going to go opposite to the direction that the car will tend to want to go, it will tend to want to ride up the ramp there. And this friction force also has components so that’s ‘Fr’ in the Y direction, and here’s friction in the X direction. So in the Y direction you can see that we have ‘Fry’, ‘FNy’ and ‘Fg’. We have kept the coordinates as in the same by the way as in the first part, we have X straight to the left not along the ramp and we have Y straight up. So we have these three Y forces. So one is going up, the normal force Y is going up, and the friction force Y component is going down so is gravity. So in our Y direction equation, ‘F’ is equal ‘m’ times ‘a’ type of equation, we have ‘FNy’ positive minus ‘Fry’ minus gravity equals zero. In the X direction, we have the X component of friction, plus the X component of the normal force working for us in the X direction, and those two together will provide the centripetal force. So we have ‘FNx’ plus ‘Frx’ equals ’m’ times ‘v’ squared over ‘r’. Let’s rewrite these equations by substituting with the trigonometry, so we have ‘FN’ cosine theta minus ‘Ffr’ sine theta minus ’m’ times ‘g’ equals zero. And in the X direction, we have ‘FN’ sine theta plus ‘Ffr’ cosine theta equals ’m’ times ‘v’ squared over ‘r’. Now we have two equations and two unknowns, this is the systems of equations and we’re going to solve the equations with a technique called solving by addition or subtraction. So let’s first solve for ‘FN’ which means we want to make the friction terms the same. So to find ‘Fn’: the Y direction equation times cosine theta, that’s ‘FN’ cosine squared theta minus friction cosine theta sine theta minus ’m’ times ‘g’ cosine theta equals zero. And then we have the X direction equation times sine theta, and that’s going to give us ‘Fn’ sine squared theta plus ‘Ffr’ sine theta cosine theta equals ’m’ times ‘v’ squared over ‘r’ times sine theta. When we add these equations, equation one and equation two, when we add equations one and two, what’s going to happen is we’ll have the normal force times cosine squared theta from one plus the normal force times sine squared theta from equation two, the friction terms are the same so they disappear, we have a minus ’m’ times ‘g’ cosine theta from equation one equals ’m’ times ‘v’ squared sine theta over ‘r’ from equation two. ‘FN’ can be factored out of the cosine squared and the sine squared meaning that we have the ‘FN’ alone there, these add up to one because sine squared plus cosine squared is always one, that’s a trigonometric identity. And since we write this equation knowing that, we have: ‘FN’ equals ’m’ times ‘v’ squared sine theta over ‘r’ plus ’m’ times ‘g’ sine theta. It hasn’t quite entirely answered the question though because we want to find the coefficient of friction, and that’s the ultimate question here. So we are going to have to all this again, but the next time solving for the friction force and then we’ll say that the friction force equals ‘µ’ times ‘FN’ and knowing the friction, and knowing that ‘FN’, we can then solve for ‘µ’. So we have the original Y direction formula, we’re going to multiply that by sine this time because our target is this ‘FN’, we’ll take the Y direction equation multiply it by sine and the X direction equation multiply it by cosine, and when we subtract the equations, they’ll disappear leaving us with only the friction force terms. Let’s call this equation three. We have the Y direction equation times sine theta, that makes ‘Fn’ sine theta cosine theta minus ‘Ffr’, sine squared theta minus ’m’ times ‘g’ sine theta equals zero. And equation four is the X direction equation times cosine theta. We have ‘FN’ sine theta times cosine theta plus ‘Ffr’ times cosine squared theta equals ’m’ times ‘v’ squared cosine theta over ‘r’. We’ll take equation four minus equation three and that will give the ‘Ffr’ times sine squared theta plus cosine squared theta plus ’m’ times ‘g’ sine theta equals ’m’ times ‘v’ squared cosine theta over ‘r’. sine squared theta plus cosine squared theta again is one because that’s a trig identity, and we solve for the friction force: ‘Ffr’ equals ’m’ times ‘v’ squared cosine theta over ‘r’ minus ’m’ times ‘g’ sine theta. So we say that the friction force is ‘µ’ times ‘FN’ and that means that ‘µ’ equals friction force divided by normal force. So we have ’m’ times ‘v’ squared cosine theta over ‘r’ minus ’m’ times ‘g’ sine theta all of that is being divided by the normal force equation, ’m’ times ‘v’ squared sine theta over ‘r’ plus ’m’ times ‘g’ cosine theta. ‘m’ is a common factor between the numerator and the denominator so it cancels. There’s two more steps: we’re going too write that ‘µ’ is ‘v’ squared cosine theta over ‘r’ minus ‘g’ sine theta divided by ‘v’ squared sine theta over ‘r’ plus ‘g’ cosine theta. Let’s substitute in some numbers now and get our answer: we know that ‘v’ is twenty six point three nine meters per second, we’ll square that, times cosine of the banking angle that we found before which is twenty six point seven zero seven eight degrees all divided by eighty eight meters minus nine point eight times sine of the banking angle twenty six point seven zero seven eight and all of that is divided by twenty six point three nine meters per second squared times sine of twenty six point seven zero seven eight all divided by eighty eight meters plus nine point eight times cosine of the banking angle twenty six point seven zero seven eight. And that works out to zero point two one six which is rounded to zero point two two and there are no units for the coefficients of friction. If you’re using the 5th Edition, the only change is twenty five meters per second and the banking angle will work out to twenty five point seven four four eight and change that here, twenty five, twenty five, and this is twenty five. So let me write this twenty five point seven four four eight, twenty five point seven four four eight and so on. And your answer after also changing the radius of curvature which is eighty meters in the 5th Edition is zero point two three after rounding. So you can go back and change the numbers in our first stage as well or you’re just finding the normal force when there is no friction and you had a different speed. Your speed here was nineteen point four four four meters per second and then that works out to the different banking angle of twenty five point seven four four eight.