VIDEO TRANSCRIPT

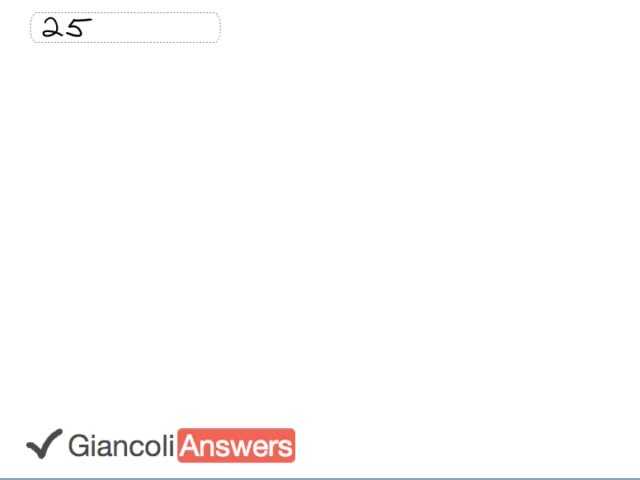
So in this problem we need to find the tangential component of the net force and the radial component also known as the centripetal component. And the example gives us the tangential and the radial accelerations. So we’ll write those down with the tangential component of the acceleration along the circle is three point two meters per second squared. This is the component of the acceleration that means it’s actually increasing its speed along the circle whereas the radial component of acceleration also known as the centripetal acceleration is zero point four five meters per second squared. The tangential force then is going to be ‘F’ equals ‘m­’ times ‘a’ and so mass times the tangential component of acceleration. Putting in numbers we have one thousand one hundred kilograms times three point two meters per second squared gives us three point five times ten raised to power three newtons. The radial component of the force is going to be mass times the radial acceleration, one thousand one hundred kilograms times zero point four five meters per second squared that is five point zero times ten raised to power two newtons. So these are the 6th Edition answers, for the 5th Edition you would instead have to substitute one thousand kilograms here and that would give an answer three point two times ten to the three Newtons and one thousand kilograms here would instead give the 5th Edition an answer of one point eight times ten to the three Newtons.