VIDEO TRANSCRIPT

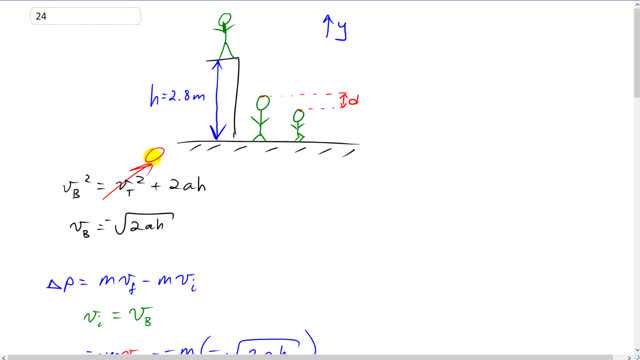
This is Giancoli Answers with Mr. Dychko. To figure out the impulse that this person experiences at the bottom of the cliff, we need to know what speed the person will have there and we'll use kinematics to figure that out knowing that the velocity at the bottom of the cliff squared equals the velocity at the top of the cliff squared plus 2 times acceleration times the displacement or the height of the cliff here. And at the top of the cliff, they have zero velocity and so take the square root of both sides and we get that the velocity at the bottom of the cliff is square root 2 times acceleration times height of the cliff. Now for the impulse, the final momentum is gonna be zero because they come to a stop and the initial momentum is that momentum where they have just at the moment that they are beginning to contact the ground so there's two intervals of time in this question which could be a source of confusion; first is the interval of time during which they are falling from the cliff and we have already dealt with that here and we are done with that and now we turn our attention to this interval of time when they are just contacting the ground and coming to a stop. So the impulse that we are calculating is the impulse during this time when they just begin contacting the ground and they come to a stop so their final velocity is zero and initial velocity is what we have calculated here at the bottom of the cliff; negative square root 2ah. So that's what we say here initial velocity is at the bottom of the cliff and we substitute that into here knowing that this term is zero and we get the impulse is negative mv B. So that's negative m times negative square root 2ah and in retrospect, I probably should have chosen down to be the positive direction but I have a y is positive up here so that's why there's going to be a lot of negative signs spread throughout here. So we have 55 kilograms times square root of 2 times negative 9.8 meters per second squared— acceleration due to gravity— times negative 2.8 meters—displacement from the top of the cliff— and this gives 410 kilogram meters per second is the impulse and that's positive because the impulse is in the upwards direction. Now for calculating the force on the person, we'll use that the net force equals impulse over time and in this question, it's important to realize that this formula is net force; it's not just, I mean normally, you just write the letter F for force but but it's always net force and that's important here because when this person is in their crouch coming to a stop, there is the force applied upwards on them and there's also a force downwards due to gravity and it's the force up that we have to calculate and it's the net force that this formula gives us so knowing that distinction is important and we'll take that the net force is the up force minus the down force and then we'll solve for the up force by adding F g to both sides here and we get that the up force is the net force plus gravity. So that's getting a little ahead of things, let's step back a second. To figure out the time, we need to use kinematics we already have the impulse from part (a) and we'll use this kinematics formula here that the displacement of the crouch is gonna be the average velocity during the crouch multiplied by the time of the crouch and so we know how much the crouch is— in part (b), it's 1 centimeter and in part (c), it's 50 centimeters— and we know the velocities involved too— the final velocity is zero because they come to a stop; the initial velocity is the velocity at the bottom of the cliff— and so we are gonna solve this for t. And we have d is v it over 2, multiply both sides by 2 over v i and you get that time is 2d over v i. So we'll plug that into the net force formula in a moment; first, we'll just start from the beginning and say that net force is impulse over time and impulse is the change in momentum so final momentum minus initial momentum, there's no final momentum so we have that the net force is negative mv i over t. And now we'll plug in for t and instead of dividing by t, we'll multiply by its reciprocal because having fractions within fractions is confusing so let's just keep it all in one line and then multiply by the reciprocal of t instead of dividing by it. So we are gonna multiply by v i over 2d and this makes v i squared and multiply it by m over 2d and there's a negative there from the formula here and then we substitute for v i knowing that it's the velocity at the bottom of the cliff as we have seen in part (a) before. So that's negative square root 2ah and when you square that, you get a 2 which cancels with the 2 in the bottom and ah and you end up with net force is negative mah over d. Now that's the net force and the net force is the sum of all forces so take the upward force and then add to that the downward force but I like to put negative signs explicit in my formula's and so I'm gonna say the total up minus the total down so F up minus F g. So take the F g to the other side by adding it to both sides and so the force up is the net force plus gravity. So then net force is negative mah over d and factor out the m and you get the force up is m times g minus ah over d so now we can finally plug in some numbers. We have that that up force is 55 kilograms times 9.8 meters per second squared minus the acceleration while falling from the cliff— negative 9.8 meters per second squared— times the displacement from the top of the cliff—negative 2.8 meters— divided by the displacement during the crouch of negative 1.0 times 10 to the minus 2 meters and that gives a force of 1.5 times 10 to the 5 newtons. And then in part (c), we do the same thing but now it's 50 centimeters crouching displacement and so we have 55 kilograms times 9.8 minus negative 9.8 times negative 2.8 divided by negative 50 centimeters or times 10 to the minus 2 meters and we end up with 3557 but there's only one significant figure in this 50 centimeter crouching distance and so we have one significant figure in our answer then. So that's 4000 newtons upwards is gonna be the force in part (c).