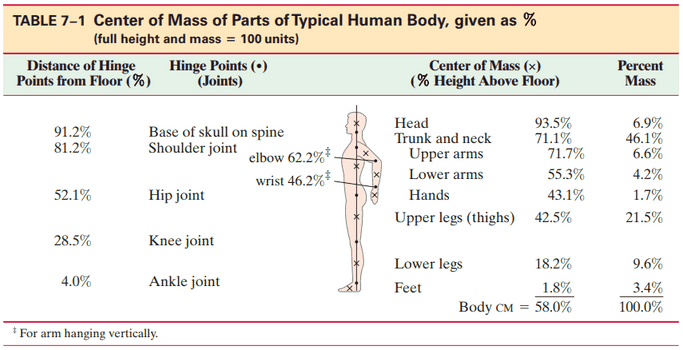
Use Table 7–1 to calculate the position of the CM of an arm bent at a right angle. Assume that the person is 155 cm tall.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. We have this arm bent at a right angle and we have to find its center of mass and it will be about here somewhere and we are gonna calculate that position by first considering the horizontal direction called x and then the vertical direction y and we'll choose our origin to be here at the shoulder and choose y to be positive in the downward direction. So we have three parts to consider; the upper arm, the lower arm and the hand. So our system consists of three parts and so that's why we have three terms in the top of this formula for calculating the x-position of the center of mass and we are gonna have the mass of each part, the mass of the upper arm here for example, multiplied by the distance to the center of mass of the upper arm plus mass of the lower arm times distance to the center of mass of the lower arm plus mass of the hand times the distance to its center of mass then divide by the total mass. So we are told that the location of the shoulder joint is 81.2 percent of the person's total height above the ground and that the position of the center of mass of the upper arm is 71.7 percent of the person's height. So taking that difference, we get 9.5 and so that's the percent of a person's total height distance from the shoulder to the upper arm center of mass. The x-position of the center of mass of the lower arm in this bent position is gonna be the difference between the shoulder joint's position minus the elbow joint's position and that's gonna be 19. And the hand has the same horizontal coordinate as the elbow and lower arm's center of mass and so we're gonna have 19 there as well. So that's why I have 19 and 19 here, multiplying each of those by the mass of the hand and the lower arm respectively and then times by the percent mass in the upper arm times its distance from the shoulder, 9.5, divided by the total masses and that gives 13.984 is the position of the center of mass in the horizontal direction and this is a percentage of a person's total height and we'll turn that into centimeters in a second. Now for the y-coordinate of the center of mass; it's the same type of story and conveniently, the y-coordinate of the center of mass of the upper arm is 0 and so that's nice—don't have to work with that too much— and then the y-coordinate of the center of mass of the lower arm is gonna be the elbow position minus the center of mass of the lower arm and that gives 6.9 is the distance below the x-axis to the center of mass of the lower arm. And then for the hand, it's elbow joint position, 62.2 minus 43.1 which gives 19.1 and so we plug those things in multiplying by whatever their related masses are and we get 4.916 and turning those into centimeters, we take these percent answers and then multiply by the person's height of 155 centimeters. So 13.984 percent of 155 is 21.67 and 4.916 percent of 155 is 7.62. So the position of the center of mass is 21.7 centimeters by 7.6 centimeters with the origin at the shoulder and downward being the positive direction.