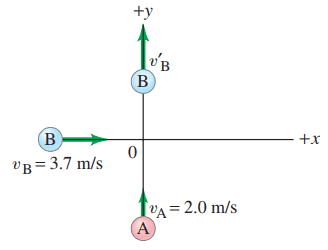
Billiard balls A and B, of equal mass, move at right angles and meet at the origin of an xy coordinate system as shown in Fig. 7–36. Initially ball A is moving along the y axis at +2.0 m/s, and ball B is moving to the right along the x axis with speed +3.7 m/s. After the collision (assumed elastic), ball B is moving along the positive y axis (Fig. 7–36) with velocity ${v^{'}_{B}}$. What is the final direction of ball A, and what are the speeds of the two balls?

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Billiard ball B is approaching this point of collision at 3.7 meters per second and billiard ball A is going along the positive y-axis at 2.0 meters per second and after the collision, we are told that ball B is going directly upwards and ball A we don't know what its direction is nor do we know its speed and we don't know the speed of ball B after the collision. So there's three things we don't know: we don't know v B prime, we don't know v A prime and we don't know Θ A Θ B we do know—90 degrees— and we know everything about before the collision. So after their collision, we have some total x-momentum and it's gonna be entirely because of ball A because ball B is is going straight upwards so it has no component of its momentum in the x-direction after the collision. So that means the total momentum in the x-direction will be the mass of ball A times its velocity after the collision times cos Θ A because cos is this adjacent component here of this momentum triangle here. And that's after the collision and then before the collision, the total x momentum is gonna be that due to ball B so it's gonna be mass of ball B times its speed—3.7—because it's entirely going in the x-direction so there's no need for any sin or cos there. Then in the y-direction, we have two balls going in the y-direction after the collision, both ball A and ball B, and at least we think so, we have to assume that maybe ball A is going somewhat up although we'll find at the end of the question that Θ A is zero so it turns out that ball A is going along the x-axis but we don't know that yet so we have to draw a picture with some Θ A there. So after the collision, we have mass B times the speed of ball B after the collision— it's going straight upwards so there's no trig needed— and its momentum is entirely in the y-direction and add to that the component of the momentum of ball A in the y-direction so sin Θ A times m Av A prime. And that total after the collision equals the total y momentum before the collision which is just that due to ball A, m A times v A. And we are also told that this collision is elastic and we need to create an equation from that piece of information because we have three things that we don't know and so whenever you have three things that you don't know, you need to have three equations to deal with that; the number of equations always has to equal the number of unknowns. So we have m Av A squared, that's the kinetic energy of ball A before the collision and here's the kinetic energy of ball B before the collision— I'm not bothering to write the one-half because that's gonna be a common factor that cancels everywhere— and that's gonna equal mass A times speed of A, after collision, squared plus mass B speed of B, after the collision, squared, okay. So the next part of this question is an algebra issue where we have to work with these three equations to get rid of the unknowns and then whittle it down to solving for one of the unknowns. So equation one we can rewrite as version b and knowing that the masses are equal, the m B's and the m A's are gonna cancel that's a common factor on every one of these terms. This is true for all these equations here. That's convenient and we can rewrite equation 1, version b as v A prime cos Θ A equals v B. I switched the sides around because I have a strategy in mind here where I'm gonna take this cos Θ A and this sin Θ A and make them disappear by squaring this equation and this equation and adding them together, I'll show you what I mean in a second but first equation 2, we'll solve it for v A prime sin Θ A by taking this v B prime to the other side that makes it v A minus v B prime. And then switch the sides around so you have v A prime sin Θ A equals v A minus v B prime. So the tricky business here is knowing that sin of any angle squared plus cos of that same angle squared equals 1. and the reason that's gonna be useful is because we can take each of these equations— equation 1b and equation 2b— we can square each of the equations and then add together those squares and we'll see that we have v A prime squared times cos squared Θ A when we square the left hand side here and plus v A prime squared sin squared Θ A and this v A prime squared is a common factor between these two terms here so we factor it out and it ends up being v A prime squared times cos squared plus sin squared which is the number 1 and so we are left only with v A prime squared on the left side; that's the Pythagorean identity for trigonometry. And then on the right hand side here, not much we can do, we have to square the right hand side of equation 1b so that's where this v B squared comes from and then we square the right hand side of equation 2b and that gives v A squared minus 2 times v Av B prime plus v B prime squared. So where's the next step here; the next step is to consider the energy equation and rewrite it by solving it for v A prime squared. So we have two equations for v A prime squared and that will be useful because then we can say that this equation equals this equation. And so that's the energy equation; this term goes to the left hand side which makes it a minus v B prime squared so that's v A squared plus v B squared minus v B prime squared and then switch the sides around so we have v A prime squared on the left and then equate the two. This is v A prime squared and this also is v A prime squared so they are equal to each other. So I have substituted from the energy equation into v A prime squared here and written v A squared plus v B squared minus v B prime squared equals this part copied there. Now we'll reduce some things here; we subtract v B squared from both sides, subtract v A squared from both sides move this term to the left hand side which makes negative 2v B prime squared equals negative 2v Av B prime and then divide both sides by 2v B prime and you get v B prime equals v A. So and then you can substitute into this energy formula here to solve for v A prime squared and v A prime squared is v A squared plus v B squared and then minus v B prime squared but now I just figured out that v B prime is v A so that means it's minus v A squared and so these make zero and so then v A prime equals v B. So they have exchanged velocities in other words; the velocity of ball B after the collision is— well, I guess I shouldn't say velocity, I should say speed because the directions are a little different— so v B prime equals v A. Well, you could say velocities are sort of exchanged too, couldn't you, because we can see it from down here that when we plug into the equation for sin Θ A based on this one up here, we can solve for sin Θ A equals v A minus v B prime divided by v A prime. Since v B prime is v A, this numerator is zero so Θ A is zero. So the ball A goes in the direction after collision that ball B was initially. So they have exchanged velocities entirely, both speed and direction. So ball A goes to the right with a speed of 3.7 and ball B goes straight up with a speed of 2.0 after the collision.