
A 100-W lightbulb has a resistance of about when cold and when on (hot). Estimate the temperature of the filament when hot assuming an average temperature coefficient of resistivity .
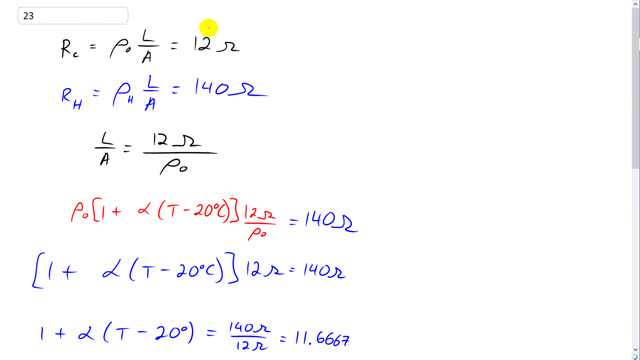
In order to watch this solution you need to have a subscription.
This is Giancoli answers with Mr. Dychko. The resistance of this filament when it's cold at 20 degrees Celsius is gonna be the resistivity at 20 degrees Celsius times the length of the filament wire divided by its cross-sectional area. And we're told that's 12 ohms. And then when the filament is hot we have some hot resistance, subscript ‘H’ for hot and that's going to be the new resistivity when it's hot, times the same length divided by the same area. And that equals a 140 ohms and from this equation here we can solve for L over A, length over area, and that's 12 ohms divided by the resistivity at 20 degrees and then substitute that in for L over A in the R H formula. And that's why we have 12 ohms over P naught here. And then also I substituted for the resistivity when hot and that's gonna be the resistivity at 20 degrees, that times one plus the temperature coefficient of resistivity times the change in temperature at final temperature minus the initial temperature of 20. And all that equals a 140 ohms because I substituted it into this formula for both the L over A and the Rho H. So. the Rho naught cancels there and we have one plus alpha times T minus 20 times 12 ohms equal 140 ohms and divide both sides by 12 ohms. And here one plus alpha times T minus 20 equals 140 over 12 which is 11.6667 and then subtract one from this side and one from this side and you get alpha times T minus 20 is 10.6667 and divide both sides by Alpha and you get T minus 20 equals 10.6667 over Alpha and then add 20 to both sides. And you get the temperature is 10.6667 divided by 0.0045. Because that's what alpha is, plus 20 degrees Celsius which is 2900… oh, 2390.4 degrees Celsius or about 2.4 times ten to the three degrees Celsius. So that must be the temperature when the filament is hot given that its resistance has increased up to 140 ohms. That's the temperature that it must have.