
A small immersion heater can be used in a car to heat a cup of water for coffee or tea. If the heater can heat 120 mL of water from to in 8.0 min,
- approximately how much current does it draw from the car’s 12-V battery, and
- what is its resistance? Assume the manufacturer’s claim of 85% efficiency.
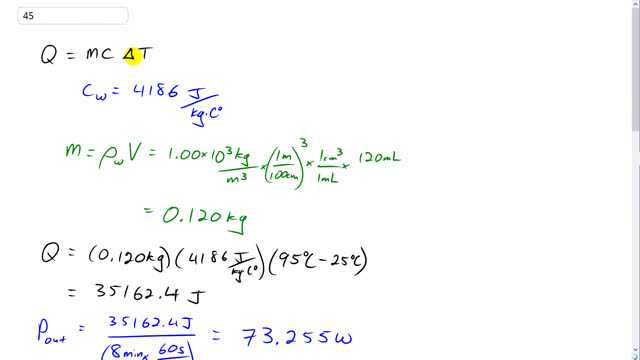
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The amount of heat that’s given to the cup of water, or coffee, or tea, or whatever it is, is the mass of water times the specific heat of water times its change in temperature. This Q here has nothing to do with Coulombs, it has nothing to do with the charge. This is the same letter Q used for heat in chapter 13 or so we're in that was. The specific heat of water is 4,186 Joules per kilogram-Celsius degree. The mass of the water is density of water times its volume. Now, there’s 120 milliliters in the cup, and we multiply that by one cubic centimeter for every milliliter, and then convert this into cubic meters by going one meter for every 100 centimeters cubed, and then we multiply by the density of the water, 1 times 10 to the 3 kilograms per cubic meter. We have 0.120 kilograms of water. The amount of heat transferred to the water is the mass 0.12 kilograms times the specific heat of water, 4,186 Joules per kilogram-Celsius degree times the change in temperature, 95 degrees Celsius, final temperature minus 25 degrees Celsius that we started at. So it’s 35,162.4 Joules. The power output of this immersion heater is that amount of heat given to the water divided by the time it takes to do it. It’s divided by 8 minutes converted into seconds by multiplying by 60 seconds per minute at the bottom. That’s 73.255 watts. The efficiency of the immersion heater is the power output divided by the power input, and we're told that's 0.85. The power input, this is the power consumed by the immersion heater to do its work, to do its job of power output. It's gonna be power output divided by 0.85. Take this and multiply both sides by P in divided by 0.85. And on the right side by P in, and the left side, the P ins will cancel leaving us with i>P out over 0.85 and then switch the sides around. So the power consumed by the immersion heater is 73.255 watts power output divided 0.85 which is 86.182 watts. We take this power input consumption by the immersion heater. Divide both sides by V in this formula here. The power input is the current consumed multiplied by voltage, divide both sides by V and you get the current. That's the power input divided by V. That's 86.182 watts divided by 12 volts, which is 7.2 amps. The resistance of the immersion heater, we can calculate using this formula. We have power input equals the voltage divided by the resistance, and multiply both sides by R over P, and you get that the resistance is voltage squared divided by the power consumed. That's 12 volts squared divided by 86.182 watts which is 1.7 ohms.