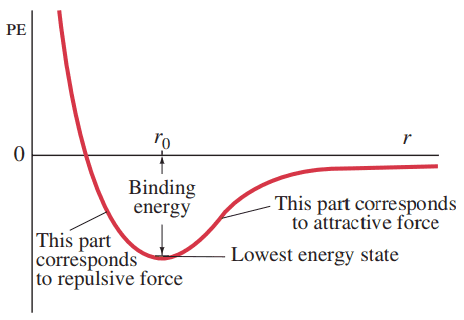
is the separation of the two H atoms. The binding energy (the energy difference between PE = 0 and the lowest energy state near the bottom of the well) is 4.5 eV, and

r_0 = 0.074 \textrm{ nm}

$\Delta E = 1.5 \times 10^{-2} \textrm{ eV, } \lambda = 82 \; \mu \textrm{m}$
$\Delta E = 3.0 \times 10^{-2} \textrm{ eV, } \lambda = 41 \; \mu \textrm{m}$
$\Delta E = 4.5 \times 10^{-2} \textrm{ eV, } \lambda = 27 \; \mu \textrm{m}$

Find us on:

Giancoli Answers, including solutions and videos, is copyright © 2009-2022 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.

The equilibrium separation of H atoms in the H2\textrm{H}_2H2​ molecule is 0.074 nm (Fig. 29–8). Calculate the energies and wavelengths of photons for the rotational transitions

Find us on:

The equilibrium separation of H atoms in the $\textrm{H}_2$ molecule is 0.074 nm (Fig. 29–8). Calculate the energies and wavelengths of photons for the rotational transitions