
What is the area, and its approximate uncertainty of a circle of radius ?
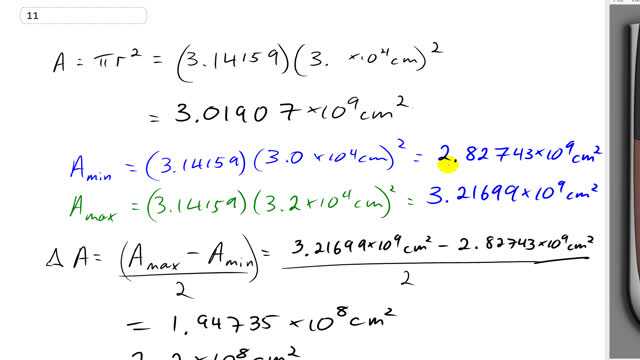
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We are going to estimate uncertainty by calculating what the maximum possible area would be of this measurement within its uncertainty and then the minimum area value and then check the difference between the two, divide by 2 to get this spread or the absolute uncertainty in our area measurement and then go from there. So this is the straightforward calculation to begin with is πr squared to calculate the area of the circle and we get 3.01907 times 10 to the 9 centimeter squared. And then we are not actually given what the uncertainty is and so we just have to make an assumption at least it's going to be the very minimum plus or minus 1 of the most precise digit and that's the tenths place, you know, in this number here— it's actually the ten thousandths place when you expand it with times 10 to the 4 but never mind— it's just this digit here is going to be plus or minus 1 and so the minimum possible area with an uncertainty would be π times 3.0 times 10 to the 4 centimeters and then we get this number. And then the area could be as high as π times 3.2 times 10 to the 4 centimeter squared and you get that and then the difference of the spread—the ΔA— is gonna be this maximum minus the minimum and then take half of that total difference to get 1.9473 times 10 to the 8 centimeter squared which can just be 2; you only have one significant figure in any error estimate because it is just an estimate there's no precision in how we came up with this number, it was just an assumption that we used to get it in the first place and at most, you can have two significant figures in a error estimate but in this case, we have no basis other than just our regular assumptions here that this is plus or minus 1 and so yeah one significant figure is all we are entitled to here. And then we are gonna actually change this to 2 or 0.2 times 10 to the 9 that just makes things a little cleaner in our final answer because our final answer is times 10 to the 9, it's gonna be 3.0 times 10 to the 9 and it's nice to have this 3.0 in brackets with the uncertainty of 0.2 and in order to put the uncertainty within the brackets, we have to have it also be multiplied by 10 to the 9 and so we'll and so if we are gonna have this multiplied by 10 in order to make it 10 to the 8 times 10 makes 10 to the 9, we'll have to divide this thing by 10 as well so that in fact we are not changing the quantity and then 2 divided by 10 is how we come up with the 0.2. So there we go. 3.0 times plus or minus 0.2 all times 10 to the 9 centimeter squared is our area measurement.
why do you assume the uncertainty of radius is 0.1 ?