
The speed of an object is given by the equation , where refers to time.
- What are the dimensions of A and B?
- What are the SI units for the constants A and B?
b)
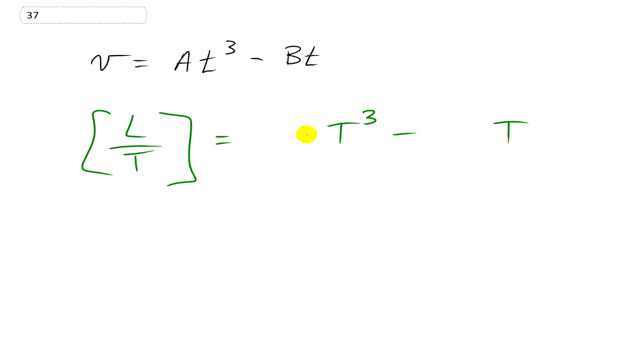
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The dimensions of velocity are length per time and so in this formula, we have time cubed in this first term and so we'll need to multiply that time cube by length over a time to the power of 4 in order to end up with length over time as the dimensions of this first term because this T cube in the top and T to the fourth in the bottom will work out to just T to the power of 1 in the bottom which is what we need. So these are the dimensions of A. So A has dimensions length over time to the power of 4. In the case of B, we need to multiply this time by a length over T squared in order to have length over time as the final dimensions of this second term. So B has dimensions length over time squared. So that's the answer for part (a). And then part (b), writing this with SI units would be length which is typically in meters and time is in seconds so that's meters per second to the power of 4 for A and then for B— this coefficient B— would be meters per second squared would be the SI units.
can you help me explain this? does (L/T^4)T^3 give you L/T?
Yes gheewala_jen4u, you got it, . We multiply each term by whatever units are necessary to end up with .
the question asks for the dimensions of A and B and you only gave us A
Ah yes, the quick answer was missing B. It's in the video, but I've added it to the quick answer now also. Thanks for spotting that.