Giancoli 7th Edition, Chapter 1, Problem 39

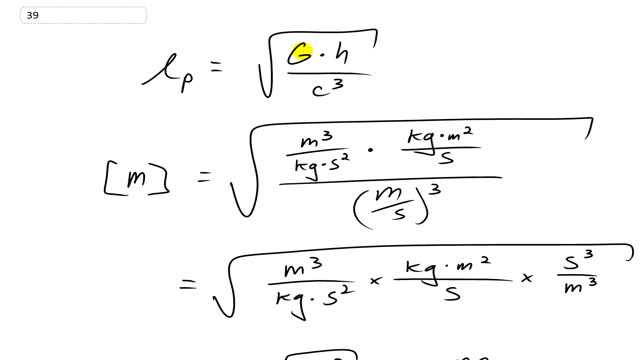
The smallest meaningful measure of length is called the Planck constant, and is defined in terms of three fundamental constants in nature: the speed of light

c = 3.00 \times 10^8 \textrm{ m/s}

, the gravitational constant

G = 6.67 \times 10^{-11} \textrm{ m}^3\textrm{/kg.s}^2

, and Planck’s constant

h = 6.63 \times 10^{-34} \textrm{ kg.m}^2\textrm{/s}

. The Planck length

l_P

is given by the following combination of these three constants: \begin{equation} \large l_P = \sqrt{\dfrac{Gh}{c^3}}. \end{equation} Show that the dimensions of

l_P

are length [L], and find the order of magnitude of

l_P

. [Recent theories (Chapters 32 and 33) suggest that the smallest particles (quarks, leptons) are "strings" with lengths on the order of the Planck length,

10^{-35} \textrm{ m}

. These theories also suggest that the "Big Bang," with which the universe is believed to have begun, started from an initial size on the order of the Planck length.]

Giancoli 7th Edition, Chapter 1, Problem 39 solution video poster

In order to watch this solution you need to have a subscription.

View sample solution

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So Planck length is given as a square root of the gravitational constant times by the Planck's constant divided by the speed of light cubed. The dimensions for capital G are meters cubed over kilogram seconds squared; dimensions for Planck's constant is kilograms times meters squared over seconds and then divide that by the speed of light— meters per second cubed— and take the square root of that whole result. And we are gonna check to see well, I kind of made an assumption here that the Planck length is gonna have dimensions of meters because it's a length but anyway, I suppose we don't know that we are just gonna figure out what this all works out to. It's confusing to have fractions within fractions so let's sort that out by just copying this top part here I just copied this here and then dividing by this fraction is the same as multiplying by its reciprocal so we can have everything on one line. So instead of dividing by meters per second cubed, we are gonna multiply it by seconds cubed over meters cubed and that will make things a little easier to look at. And we have that the meters cubed here cancels with these meters cubed; this kilogram cancels with this kilogram; this seconds squared plus this second makes second cubed in the bottom canceling with this second cubed in the top leaving us with square root meter squared which is meters.

Find us on:

Giancoli Answers, including solutions and videos, is copyright © 2009-2022 Shaun Dychko, Vancouver, BC, Canada. Giancoli Answers is not affiliated with the textbook publisher. Book covers, titles, and author names appear for reference purposes only and are the property of their respective owners. Giancoli Answers is your best source for the 7th and 6th edition Giancoli physics solutions.