GiancoliAnswers

You are here

  4. Problem 6
Select a problem
Question: 

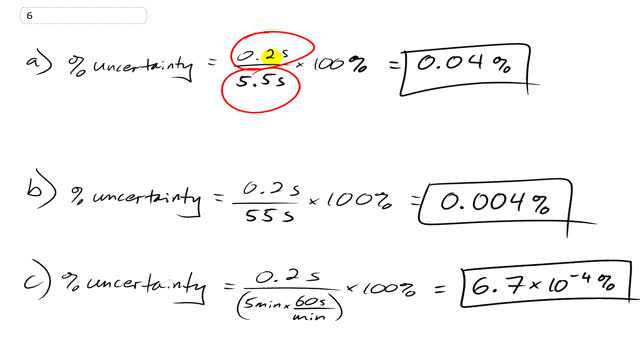
Time intervals measured with a stopwatch typically have an uncertainty of about 0.2 s, due to human reaction time at the start and stop moments. What is the percent uncertainty of a hand-timed measurement of

  1. 5.5 s,
  2. 55 s,
  3. 5.5 min?

Source: Giancoli, Douglas C., Physics: Principles with Applications, 7th Edition, 2014.

Quick Answer: 

a) $4 \%$
b) $0.4 \%$
c) $0.06 \%$

Error in the video: I mistakenly wrote fractional errors instead of percent errors. The answers written above are correct, not the answers in the video, although the working in the video is correct.

Giancoli 7th Edition, Chapter 1, Problem 6

(1:15)

Chapter 1, Problem 6 is solved.

View sample solution

Transcript for this Giancoli solution

This is Giancoli Answers with Mr. Dychko. Percent uncertainty is calculated by dividing the absolute uncertainty which is the uncertainty in the same units as your measurement— 0.2 seconds in this case is the absolute uncertainty— divided by the measurement in part (a) of 5.5 seconds and 0.2 divided by 5.5 times a 100 to turn it into a percent is 0.04 percent uncertainty. In part (b), it's 0.2 seconds divided by 55 seconds and this same uncertainty of 0.2 seconds should matter less when you have such a long measurement of 55 seconds as compared to only 5.5 seconds and the percent uncertainty reflects that. So it's 0.004 percent uncertainty which is a much smaller percent uncertainty than you had in part (a). In part (c), we are dividing by 5 minutes; now we have to make the units the same so on the denominator we have 5 minutes times 60 seconds per minute and the minutes cancel giving us this many seconds and this percent uncertainty is 6.7 times 10 to the minus 4 percent uncertainty.

Comments

By sondylevykh on Tue, 03/10/2015 - 18:42

These answers are all miscalculated. i'm looking at the book now, it has different results.

By Mr. Dychko on Tue, 03/10/2015 - 21:30

Hi sondylevykh, thanks for spotting the errors here. I was writing fractional error rather than percent error, so the answers are off by a factor of 100. I've flagged this video for a re-do, and I'll put a note above it.

All the best,
Mr. Dychko