
Estimate the number of liters of water a human drinks in a lifetime.
In order to watch this solution you need to have a subscription.
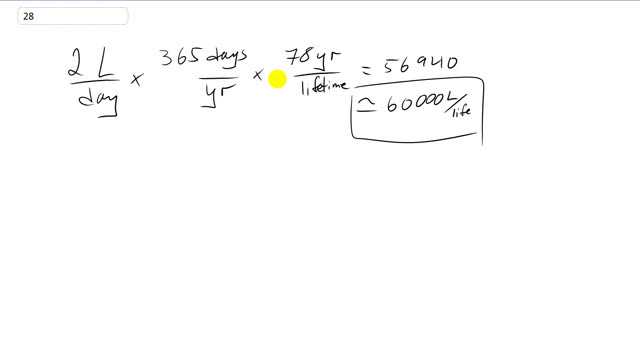
This is Giancoli Answers with Mr. Dychko. If we assume a person drinks about 2 liters of water per day and multiply that by 365 days per year and a person has an average life expectancy maybe of 78 years we'll get 60000 liters of water per lifetime. And you can see the units canceling here we have 2 liters per day and the days cancel and then the years cancel here so we are left with 2 with number of liters per lifetime so 60000 liters per lifetime.
Why your not estimating the Numbers 362 and 76 to one SIGFIG. ?
Hello, these are good questions. 365 days / year is a definition, so it's precise to three significant figures. 78 years / lifetime is an estimate, and personal opinion says that being precise to the "ones" place is appropriate, but it's just an opinion. Keep in mind that you never round numbers until the final answer. If you round before, even if a number such as 78 should be 80 since it has one significant figure, suppose, you would still nevertheless do calculations with 78, not 80. Only final answers get rounded, otherwise your calculation has an intermediate rounding error, which is to say that the calculation will be dramatically different only on account of rounding, not because any quantities have actually changed.
Hope that helps,
Mr. Dychko
Ok That is good idea
but remember the example (Example 1–6) (How much water is in this lake?) in the book . he is rounded the value of pi to 3
is he rounded for to be 1 SIGFIG or other reason since pi is also in term of (definition) as you mentioned above ?
Thanks
Hmmm, that's a thought provoking example. The goal is always to make your calculation as precise as appropriate. Avoiding intermediate rounding error is normally part of that. However, example 1-6 illustrates that if the surrounding values have only one significant figure, as is the case with educated guesses, having only one significant figure in pi is acceptable since, in this context, greater precision isn't called for on account of the other imprecise quantities in the calculation. Think of these significant figure rules as guidelines which are open to interpretation, not as firm rules.
All the best,
Mr. Dychko