
Estimate the order of magnitude (power of 10) of:
- ,
- ,
- , and
- .
b)
c)
d)
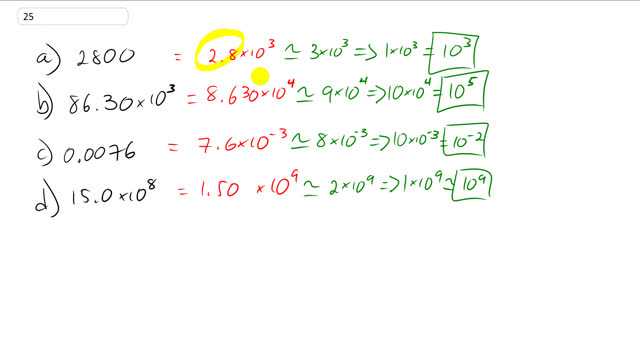
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. To turn a number into its order of magnitude, we have to write it first in scientific notation and then round that this into one single digit and then round that into either a 1 or a 10 depending on what it's closer to and then do this multiplication here to figure out our answer for the order of magnitude. So easier to show by example so let's explain each of these. 2800 in scientific notation we have to divide by 10 to the 3 to move this decimal point which is here— three spaces to the left— and then compensate for that by multiplying by 10 to the 3 I'm just explaining how to do scientific notation here so we have 2.8 because we divided by 10 to the 3 and then we have to make up for that division by multiplying by 10 to the 3 so that in fact we have only multiplied by 1 but it looks different, looks like 2.8 now and it's times 10 to the 3. This 2.8 rounds to 3 and 3 is closer to 1 than it is to 10 so we'll write a 1 there instead and 1 times 10 to the 3 is 10 to the 3; the order of magnitude is 10 to the 3. Then for 86.30 times 10 to the 3, we have to divide by 10 to the power of 1 to move this decimal point once to the left and then multiplied by 10 to the 1 to make up for that. So we have 10 to the 3 times times 10 to the 1 makes 10 to the 4 8.6 rounds to one single digit 9 and 9 is closer to 10 than it is to 1 so we'll write a 10 there instead and 10 times 10 to the 4 is 10 to the 5 so the order of magnitude is 10 to the 5. This in scientific notation we have to move this three digits to the right by by multiplying by 10 to the 3 and then divide by 10 to the 3 as well to make up for that but dividing by 10 to the 3 is the same as multiplying by 10 to the minus 3 because the negative sign in a exponent is the same as reciprocal so if you have some number divided by 10 to the 3, it's the same as saying that same number multiplied by 10 to the negative 3. So that's when I divided by 10 to the 3 here that's why I can write it as 10 to the negative 3 multiplication instead and this 7.6 which is what we have here now because we multiplied by the 10 to the 3 there becomes 8 when you round it to one digit and 8 is closer to 10 than it is to 1 so we'll write a 10 there instead and 10 times 10 to the negative 3 is 10 to the negative 2; that's the order of magnitude, 10 to the minus 2. 15.0 times 10 to the 8 is the same as 1.50 times 10 to the 9 1.5 rounds to 2 and 2 is closer to 1 than it is to 10 so we have 1 times 10 to the 9 which makes 10 to the 9 is the order of magnitude here.
hi I've a question
How we gona apply this idea with this Number 3.0*10^0
Thank You
Hi abgoooor201596, has 2 significant figures.
Cheers,
Mr. Dychko