
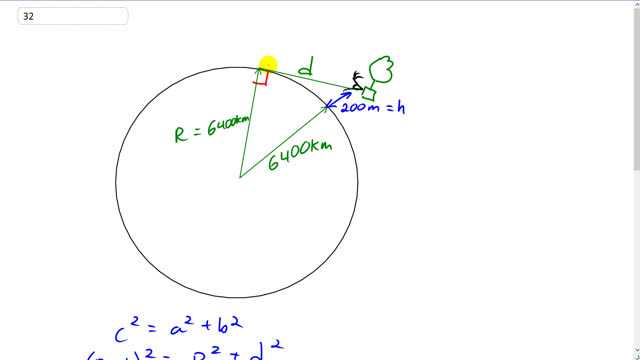
You are in a hot air balloon, 200 m above the flat Texas plains. You look out toward the horizon. How far out can you see—that is, how far is your horizon? The Earth's radius is about 6400 km.
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Looking out from a point 200 meters above the flat Texas plains in a hot air balloon, well, your line of sight is along this line here towards the horizon and as this line of sight just touches the horizon, it's making a tangent to this circle which is the Earth. And your distance from the center of the Earth is gonna be the Earth's radius of 6400 kilometers plus this 200 meters of altitude you have above the ground and we can see a triangle here and the question is asking us for the distance to the horizon. So that's this distance d from your eyes along the line of sight to where the line of sight just is tangent to the Earth here. So we have a right triangle because the tangent radius angle is always 90 degrees and so we have this leg of the right triangle— 6400 kilometers— this is the distance we are trying to find this distance, d, and then the hypotenuse is Earth's radius plus 200. So we have c squared equals a squared plus b squared so let's just imagine that c there and this side is maybe a and this is b. So we'll plug in radius plus height, R plus h— where R is the radius of the Earth— R plus h squared, that's this radius plus your height above the ground all squared equals the Earth radius squared plus the distance of the horizon squared. And squaring this bracket we end up with R squared plus 2 times R times h plus h squared equals the right-hand side and the R squared's cancel because you can subtract R squared from both sides and we are left with, after you switch the sides around, d squared equals 2 times R times h plus h squared. h is 200 meters but we'll have to turn that into kilometers in order for it to work with the other parts of this equation which are in kilometers. So that's 200 meters times 1 kilometer for every 1000 meters and that's 0.200 kilometers. So d, after you take the square root of both sides, is square root of 2 times 6400 kilometers— radius of the Earth— times 0.200 kilometers—distance above the Earth— plus the 0.200 kilometer squared and square root that whole result and you get about 51 kilometers is the distance to the horizon.