GiancoliAnswers

You are here

  4. Problem 17
Select a problem
Question: 

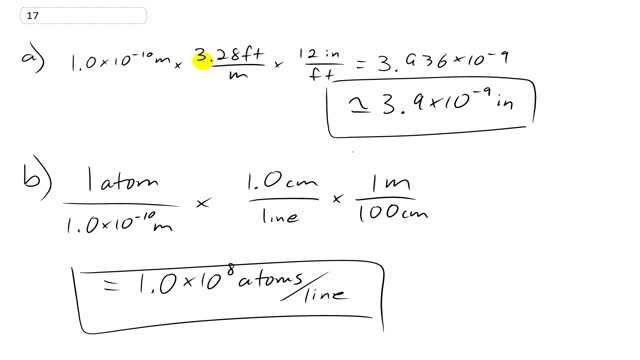
A typical atom has a diameter of about $1.0 \times 10^{-10} \textrm{ m}$.

  1. What is this in inches?
  2. Approximately how many atoms are along a 1.0-cm line, assuming they just touch?

Giancoli, Douglas C., Physics: Principles with Applications, 7th Ed., ©2014. Reprinted by permission of Pearson Education Inc., New York.
The question will be visible after logging in, as required by Pearson Education Inc.

Quick Answer: 

a) $3.9 \times 10^{-9} \textrm{ in}$
b) $1.0 \times 10^8 \textrm{ atoms/line}$

Giancoli 7th Edition, Chapter 1, Problem 17

(1:30)

Chapter 1, Problem 17 is solved.

View sample solution

Transcript for this Giancoli solution

This is Giancoli Answers with Mr. Dychko. The diameter of 1 atom is about 1.0 times 10 to the minus 10 meters and we have a conversion factor on the front cover of the textbook telling us how many feet there are per meter—3.28 feet per meter— and the meters will cancel here and we are left with feet but we want inches so we know there's 12 inches per foot and so the feet cancel leaving us with inches and this gives us 3.9 times 10 to the minus 9 inches; two significant figures in our answer because we have two significant figures in this estimate of the diameter of a typical atom. In part (b), we know that we want atoms per line as our final units and the piece of information that we start with is that there's 1 atom for every 1.0 times 10 to the minus 10 meters and so then we need to introduce some conversion factors that will cancel away the units we don't want and introduce the units we do want. So we wanna have lines in our denominator so we know that there's 1 centimeter per line and so this takes care of having lines in the denominator but there's a conflict here; this centimeters and the meters are not the same so they don't cancel and so we need to introduce this conversion factor— there's 1 meter for every 100 centimeters— and so that takes care of this centimeters here and then the meters here cancel leaving us with atoms per line. So it's 1.0 times 10 to the 8 atoms per line.

Comments

By harringtonwarri... on Mon, 09/07/2015 - 11:21

could you please tell me how you got to 1.0*10^8? looking the problem you laid out... i see 1.0*10^-10/100.... which does not equal your solution?

By Mr. Dychko on Wed, 09/09/2015 - 21:00

Hi harringtonwarriorfitness, the work in the video isn't quite how you wrote it in your comment. The problem mentions that "a typical atom has a diameter of about $1.0 \times 10^{-10} \textrm{ m}$". This can be rephrased as "one atom per $1.0 \times 10^{-10} \textrm{ m}$". That's maybe an odd way to say it since it might be more typical to say "$1.0 \times 10^{-10} \textrm{ m}$ per atom", but either way works, and mentioning the atom first puts that in the numerator of the fraction. The "one atom per $1.0 \times 10^{-10} \textrm{ m}$" can be written as the fraction $\dfrac{1 \textrm{ atom}}{1.0 \times 10^{-10} \textrm{ m}}$ and it's this fraction which was missed in your working "1.0*10^-10/100". The "1.0 atom" is on top, and it's divided by "10^-10".

Hope that helps,
Mr. Dychko