
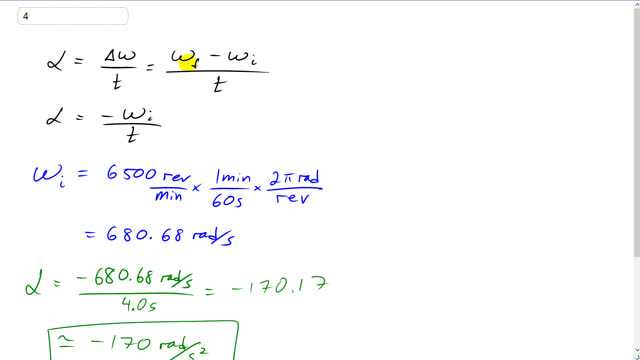
The blades in a blender rotate at a rate of 6500 rpm. When the motor is turned off during operation, the blades slow to rest in 4.0 s. What is the angular acceleration as the blades slow down?
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The angular acceleration of the blades in this blender equals the change in their angular velocity divided by the amount of time it takes for that change to happen so it's the rate of change of the angular velocity. The blade's come to a stop so their final angular velocity is zero which means that in this case that the angular acceleration is negative initial angular velocity divided by time. We need to express this angular velocity in radians per second so we'll take the 6500 revolutions per minute that it starts with times by 1 minute for every 60 seconds to get revolutions per second and then times by 2π radians for every revolution; each revolution goes through one complete circle which is 2π radians and so the revolution's cancel and we are left with 680.68 radians per second. And then we'll take that initial angular velocity and divide it by 4 seconds and we get negative 170 radians per second squared— negative meaning that it's slowing down in this case.