
A 1.80-m-long pole is balanced vertically with its tip on the ground. It starts to fall and its lower end does not slip. What will be the speed of the upper end of the pole just before it hits the ground? [Hint: Use conservation of energy.]
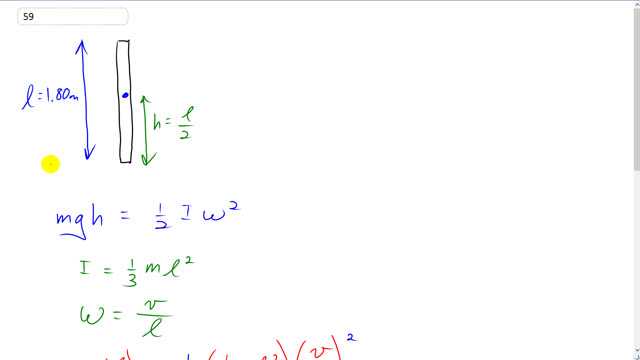
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Initially, all the energy in this rod is gravitational potential energy and we calculate that by going mass times g times the height of its center of mass above the reference level and we'll take the reference level to be the ground. And so the height will be the length divided by 2 the center of mass will be in the geometric center of the object when it's a uniform object and so the mass is distributed evenly among the whole length of the pool and so the center of mass will be right in the middle, l over 2. So we'll substitute for h down here as l over 2 in our gravitational potential energy side of this equation. Now when the pole hits the ground, the center of mass will be at the position of the ground so there will be no gravitational potential in that case but there will be rotational kinetic energy and this is like just immediately before it hits the ground of course and that will be one-half times moment of inertia times angular velocity squared. So the moment of inertia for a pole with a pivot at one end is one-third mass times its length squared. And the rotational velocity can be written as linear velocity divided by the distance from the point of rotation. So we are interested in the speed v of this end up here what will its speed be when it hits the ground and we know that ω is gonna be that speed divided by the distance from that point to the pivot point so v over l in other words. So we'll make all these substitutions here: we have h is l over 2; we have moment of inertia is one-third mass times length squared and then times this v over l in place of ω squared. So the m's cancel on both sides, the l squared's cancel here and we are left with v squared over 6 on the right side and gl over 2 on the left side. Switch the sides around, times both sides by 6 and then reduce the 6 over 2 to make 3 and square root both sides and you get v is square root 3gl. So that's square root 3 times 9.8 meters per second squared times 1.80 meters length that gives about 7.27 meters per second.
Why is kinetic energy not accounted just before it hits the ground? Also, is the velocity of the center of mass the same with the end of the pole?
Hi choianchoi, thanks for the question. Let's keep in mind that one end of the pole stays in contact with the ground. It's a pole falling over, in other words. The end touching the ground has velocity zero in that case, at all times. The other end of the pole, on the other hand, has the maximum velocity of any point on the pole. The end initially in the air has a higher linear velocity than the center of mass. Kinetic energy is accounted for, and it's the strategy for calculating the velocity of the end of the pole, but the kinetic energy formula doesn't look like what you're used to from linear problems. We don't use . Instead, we use rotational kinetic energy instead, and use that to figure out the rotational velocity, which is then used to find the linear velocity of the end of the pole.
All the best,
Mr. Dychko