A uniform horizontal rod of mass $M$ and length $l$ rotates with angular velocity $\omega$ about a vertical axis through its center. Attached to each end of the rod is a small mass $m$. Determine the angular momentum of the system about the axis.

VIDEO TRANSCRIPT

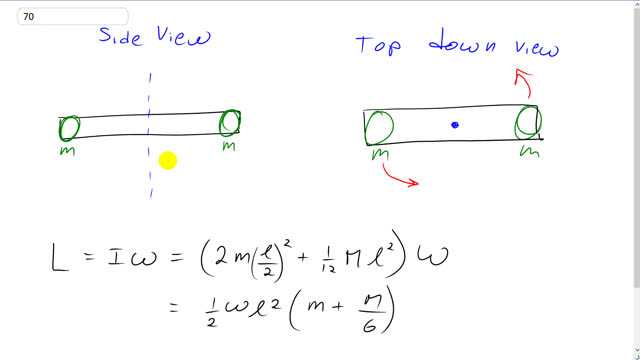
This is Giancoli Answers with Mr. Dychko. The main challenge in this question is figuring out the moment of inertia of the system. So we have a rod with an axis of rotation in its center and here's a side view and the axis of rotation is vertical and the rod is horizontal and there is a mass on each end of the rod as well. And if you have a top-down view this is what it would look like where the whole system is rotating in the direction of these red arrows. So we have a uniform rod with an axis of rotation in the center plus we have two point masses— one on each end— and each of them will have a moment of inertia mass times distance from this axis of rotation squared. So the distance to the axis of rotation is l over 2 for each of these masses—total length of the rod divided by 2. So we have two of those masses so that's why we go 2 times mr squared where r, you know, usually for point mass we have I equals mr squared so r in this case is l over 2 and that gets squared and then plus we have the moment of inertia for a rod with an axis of rotation at center one-twelfth mass of the rod times its length squared. And all that gets multiplied by the angular velocity to get the angular momentum. And so we can cancel one of the 2's here— there's two of them because it's squared— with this 2 there and then factor out the remaining one-half and factor out a half from the one-twelfth to make it into one-sixth and then factor out the l squared as well and we get one-half ωl squared times the small mass on the end plus the rod mass divided by 6 and that is the angular momentum of the system.