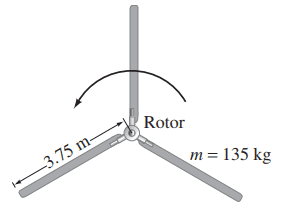
Let us treat a helicopter rotor blade as a long thin rod, as shown in Fig. 8–49.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Each of the three blades on this helicopter rotor can be considered a uniform rod with an axis of rotation at its end. So the formula is one-third mass of the rod times its length squared. Now there are three of them so the total moment of inertia is gonna be 3 times the moment of inertia of one of the rods so we have just ml squared is our total moment of inertia. So that's 135 kilograms times 3.75 meter squared and that gives about 1.90 times 10 to the 3 kilogram meter squared moment of inertia for the entire rotor. The torque required by the motor to get this thing up to speed is moment of inertia times the angular acceleration and we assume that there's no frictional torque to be concerned with here and we have already figured out the moment of inertia here so now let's just figure out α. The final angular velocity is the initial angular velocity which is 0 plus angular acceleration times time and then we'll divide both sides by t and switch the sides around and we get angular acceleration is final angular velocity divided by time. And substitute that into the torque formula for α and we get torque is moment of inertia times ω f over t and so that's 1898.4 kilogram meter squared times 6.0 revolutions per second converted into radians per second by multiplying by 2π radians for every revolution, divide by 8 seconds and you get 8.9 times 10 to the 3 newton meters is the required torque.