Problem 11

Particles of charge $+65$ , $+48$ , and $-95 \; \mu \textrm{C}$ and are placed in a line (Fig. 16–52). The center one is 0.35 m from each of the others. Calculate the net force on each charge due to the other two.

Figure 16-52.

F_1 = -1.2 \times 10^2 \textrm{ N, }

F_2 = 5.6 \times 10^2 \textrm{ N, }

F_3 = -4.5 \times 10^2 \textrm{ N}

COMMENTS

By moonpen on Wed, 3/23/2016 - 6:47 PM

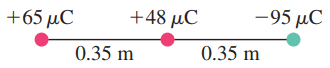
when calculating the Force of 2, why isn't the force from 2 to 1 negative?

By Mr. Dychko on Thu, 3/24/2016 - 2:46 AM

Hi moopen, thanks for the question. When calculating the net force on charge 2 we're interested only in forces exerted on charge 2. The charge 1 is exerting a force to the right on charge 2, so that force is taken as positive. It's true that charge 2 exerts a force to the left on charge 1 (this is the Newton's 3rd Law counterpart to the force exerted on charge 2 by charge 1), but this force isn't relevant since it isn't exerted on charge 2.

Hope that helps,
Mr. Dychko

By acw2085 on Sat, 1/15/2022 - 5:27 PM

It seems more intuitive to mark pushes as positive because of how the book defines attractive force as negative and positive force as repelling. Is there some other thing behind this seeming contradictory technique- for instance, does it prepare us for something later on doing it this way? Or, am I misunderstanding something?

By apelato on Mon, 1/20/2025 - 9:04 PM

why is Q3 a positive value when it states that Q3=-95uc? Is it because the negative is there solely to indicate direction rather than actual value?

By Mr. Dychko on Thu, 1/23/2025 - 8:51 PM

Hi apelato, that's a good question - thanks! Indeed, Q3 is negatively charged. The fact that it's negative informs the direction of force between it and other charges. I made a choice in my problem solving approach to sort out the direction of force resulting from the signs of the charges, put that sign (positive or negative) explicitly into the net force formula, and as a consequence use only the magnitude of each charge. The sign of the charge affects only the direction of the force, and to my way of thinking it's easier to sort this out ahead of time by specifying signs on the force terms and then use magnitudes for the charges.

For example, consider the force on Q2 due to Q3. It's to the right, so it's positive. If you were to substitute a negative for Q3 (and positive for Q2) in Coulomb's law the result would be negative which contradicts the fact that the force is positive. The sign in Coulomb's law is confusing - it doesn't indicate "left" or "right", but rather "attracting" or "repelling", so this needs to be interpreted by inspecting the geometry of the situation.

My technique is to figure out the direction of the force and put that sign in front of the force term, and then calculate the magnitude of that force by always substituting magnitudes (always positive in other words) for each charge.

Hope that helps,
Shaun

Particles of charge +65+65+65, +48+48+48, and −95 μC-95 \; \mu \textrm{C}−95μC and are placed in a line (Fig. 16–52). The center one is 0.35 m from each of the others. Calculate the net force on each charge due to the other two.

Find us on:

Particles of charge $+65$ , $+48$ , and $-95 \; \mu \textrm{C}$ and are placed in a line (Fig. 16–52). The center one is 0.35 m from each of the others. Calculate the net force on each charge due to the other two.