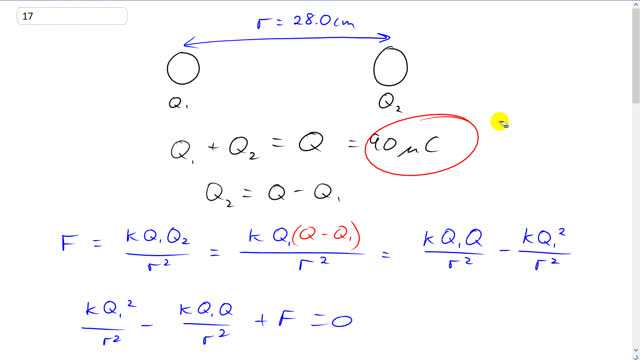
Two small nonconducting spheres have a total charge of $90.0 \; \mu \textrm{C}$.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So we know the total charge on these two spheres, and we know the distance between them is 28 centimeters. And the total charge is 90 microcoulombs. We're gonna call that total charge, Q, the charge on one of the spheres is Q₁, and then the charge in the other sphere is Q₂, and their total is Q. And we know the force of repulsion between them as well. We can write Coulomb's law like this F equals kQ₁ Q₂ over r². And we can rewrite Q₂ as the total charge minus Q₁ so that we have only one variable here, and it's Q₁. So we have to do a bunch of algebra to solve for Q₁ because we know the force, we know the distance, and we know k of course, and we know the total charge. If we multiply into the bracket here, we get kQ₁Q over r² minus kQ₁² over r². That all equals force. If we take this to the left side here, and this to the left side as well. This kQ₁² over r² term becomes positive, and we get a minus kQ₁Q over r², and we have the plus F that was there to begin with. And all that equals zero. I'm writing this in the form of a quadratic equation because that's what we're gonna have to use to solve for Q₁. Then to make it simpler, we plug into this quadratic formula. We multiply everything by r² over k. And so this terms becomes Q₁², this term becomes Q₁ times Q, and this term becomes r²F over k. So, plugging into the quadratic formular means that Q₁ is Q plus or minus square root of Q² minus four times coefficient of the squared term, which is this one, times the constant term r²F over k, all over two times this coefficient which is again, it's just one. So it's just divided by two. And plug in numbers, then you have 90 microcoulombs which is times 10 to the minus six Coulombs, plus or minus the square root of 90 times to the minus six Coulombs squared, minus four times this operation, 28.0 times 10 to the minus two meters, squared, times 12 Newtons of force repulsion, divided by Coulomb's constant of 8.988 times 10 to the nine Newton meters squared per Coulombs squared, all divided by two. And if you used a plus sign, you get this answer. And if you used a minus sign, you get this answer. The reason there's two answers is because what we can figure out here is what the charge is on one sphere and what the charge is on the other sphere but we don't know which sphere is which. And we'd get the same force of repulsion for the given, the same separation. The charge on this particular sphere has two possibilities. If the left-hand sphere is 88.8 microcoulombs then that means the right-hand sphere is 1.2 microcoulombs or vice versa. You can have the left-hand sphere, 1.2 microcoulombs, and the right-hand sphere would then be 88.8 microcoulombs. This turns into 88.8 microcoulombs because if you divide this by 10 to make it 10 to the minus six, that means then you can replace it with the prefix micro. Then to compute it for dividing by 10, you have to multiply the number by 10. And so 8.88 becomes 88.8. So 88.8 microcoulombs and 1.2 microcoulombs is the answer there. Now if the force is attractive, that means the force is negative. And so otherwise, the algebra and everything is exactly is the same, and even this formula is the same, but F is now negative 12 instead of positive 12. That's the only difference here. So I copied and pasted this line and rewrote it here with the negative 12. In which case, Q₁ becomes 9.1148 times 10 to the minus five Coulombs, or it becomes negative 1.1484 times 10 to the minus six Coulombs. This is good, we expected them to have opposite signs because since the force of attractive, the charges should have opposite signs. So, one charge is 91.1 microcoulombs, and the other charge is negative 1.1 microcoulombs. But we can't tell whether the left hand or the right hand one, which is which, but we know one is this size charge, and the other is this size charge. There we go.