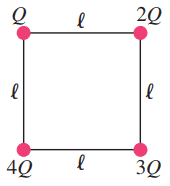
At each corner of a square of side $l$ there are point charges of magnitude Q, 2Q, 3Q, and 4Q (Fig. 16–54). Determine the magnitude and direction of the force on the charge 2Q.

VIDEO TRANSCRIPT

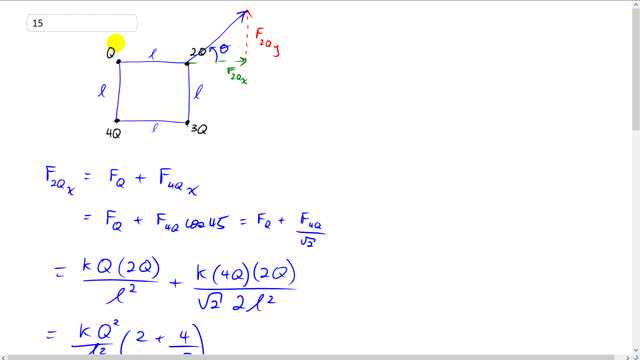
This is Giancoli Answers with Mr. Dychko. So our job is to find the net force on the charge two Q And there is a square here side length l but the charges are not the same on each corner so we have a charge of Q Here a charge of four Q In the bottom left in charge of three Q in the bottom right. So the resultant force in the charge two Q will be the vector sum of the y component of the net force and charge two Q and the x component of the force on charge two Q and it's going to have some angle theta And it's not obvious what that angle will be nor what these resulting forces will be because these charges are all of different magnitude. So it's not as easy as Question 14. So let's consider one component at a time we'll consider the x component of the force on charge two Q So there's gonna be a force due to this charge in the x direction and that part's straightforward because it's a repulsive force straight to the right and then there's gonna be no x component at all due to this charge three Q because it's forces directed straight upwards so we don't have to think about that right now. And then the force due to charge four Q is gonna have an x component and it'll have a y component. So let's find out what the x component of this force would be. So this is on the diagonal of a square which means the force direction is at 45 degrees. So here's the force due to charge four Q at an angle of 45 degrees and our interest is in knowing what this component is the x component of the four Q force and cosine of theta is gonna be the adjacent of the hypotenuse of F four Qx over F four Q And so when we rearrange this for F four Qx we can see that it's cos theta or cos 45 times F four Q now cos 45 is a special triangle 45,45, 90, one, one, two and cos 45 is one of a root two if you wanted it an exact form without using a calculator. So we have force Q Plus force four Q over root two is gonna be the x component of the force on this charge two Q and let's substitute for each of these things we have coulombs constant times one charge which is Q times the other charge which is two Q divided by the distance between them which is l squared that's the force due to charge Q on two Q and then the force due to charge four Q is gonna be coulombs constant times the four Q charge times the two Q charge divided by the distance between them which we can figure out by using Pythagoras. So this Is gonna be and this is gonna have a distance of l squared plus l squared square rooted but what we want to know is the square of that. So starting with this distance d is the square root of l squared plus l squared if you squared both sides get d squared is l squared plus l squared which is two l squared and so that's why I have two l squared here. And then the two is canceled and you can factor out the K Q squared over l squared. And you end up with just a two from this term and then you have a four over square root two in second term. And this makes 4.8284 times K Q square root over l squared. That's all we can say about the x component of the force on charge two Q because we don't know what Q or l are. So then we look at the Y component. So there is a force due to Charge three Q . Which is going to be three Q times two Q over the distance between them l squared. And then there's a force due to four Q and in the y direction but the y component is gonna be sine 45 times force four Q but sine 45 is the same as Cos 45 Also one over root two. So that's why I put a F four over root two and this is the same as it was before. Force due to four Q and factor things out and you get K Q squared over l squared times six, three times two there Plus four Over root two Because Just as before four over root two there as well. And so the only difference is that this number is now six instead of what it was before two and we expected that to be the only difference because only thing is different now is that we have this force being considered instead of this one. And this makes 8.8284 times K Q squared over l squared . So the resultant force on force on the charge two Q is the square root of the squares of both of the components that we just found. And they both have a factor K Q squared over l squared we just factor that out and square it and then multiply by the thing that's left over 8.8284 squared plus 4.8284 squared and the square root of the squared is just itself. So it’s K Q squared over l squared and then squared to these add them together to the square root of that and you get 10.1 and then And so that's the magnitude of the force 10.1 K Q squared over l squared the direction is gonna be the y component divided by the x component. And since they both have factors K Q squared over l squared those cancel and we're left with 8.8284 divided by 4.8284 and take the inverse tangent to that and we get 61.3 degrees. So we just took the inverse tangent of this force divided by this force to figure out this angle theta. And there we go force on the charge two Q is 10.1 K Q squared over l squared. 61 degrees above the positive x axis.