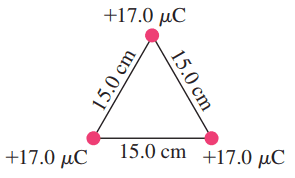
Three positive particles of equal charge, $+17.0 \; \mu \textrm{C}$, are located at the corners of an equilateral triangle of side 15.0 cm (Fig. 16–53). Calculate the magnitude and direction of the net force on each particle due to the other two.

VIDEO TRANSCRIPT

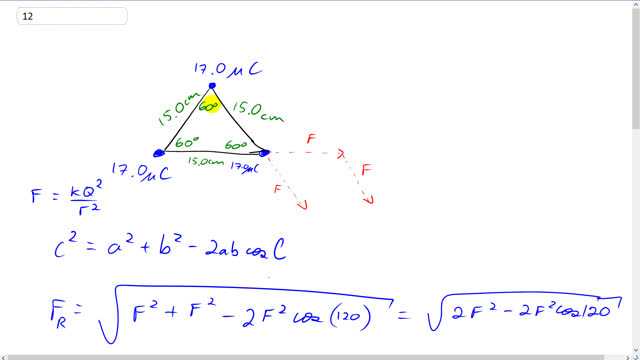
This is Giancoli Answers with Mr. Dychko. Because all the charges are the same and because the distances between each of the charges are all the same. Once you figure out the force on one charge it'll be the same magnitude force on each of the other charges. And we'll find out actually that the force is directed along a line connecting the center to the corner. We'll get to that in a second. So let's consider this bottom right charge here and there are two forces on it. One force is due to this charge here. And the force is directed along the line connecting the two charges here. And because they're both positive this force is repulsive and so it's that this is the force here on the bottom right charge due to the top charge. And then there's also this force here directed straight horizontal due to this charge. repelling this bottom right charge. So it's bottom right charge experiences two forces of equal magnitude and the direction of this force here is gonna be 60 degrees below the positive x axis. Make a coordinate system like that. This force is 60 degrees below the positive x axis because these angels are opposite and each angle in equilateral triangle is 60 degrees. so we can move this force over to here. Let's get this one out of the way and move his force over here to create our resultant force triangle here. So thats 60 degrees below the horizontal. And let's get the result into these two forces that's connecting the tale of one force to the head of the other force. This is Force resultant. And we have this triangle here where this angle here is known this angle is gonna be the straight line angle of 180 degrees minus 60 and 180 degrees minus 60 degrees is 120 degrees. So this angle up here is 120 degrees from there to there and that's useful because we can use the cosine law to figure out this resultant force. Now we could have broken each of these. We could have broken this force into its x and y components. That would be a fine technique as well. But this is the way we're gonna do it here. So cosine law says that the length of one side of a triangle equals the length of the other side squared plus the other side squared minus two times, these two sides multiplied together multiplied by the cosine of the angle opposite the side we're trying to find kind of easier to say with letters a, b and c. So let's write Nestor out of the triangle here. Hopefully you've heard of the cosine law. So here's Side a , Side b and side c and here's angle capital C and this is the angle opposite the side we're trying to find c So c squared equals a squared plus b squared which should remind you of Pythagoras and but this is this cosine law applies to any triangle not just a right triangle. And you can make that happen by going minus two times a times b times cosine of the angle opposite the side we are trying to find c . There And the force resultant is like c . So take the square root of both sides and you solve for C so force resultant is the square root of one side length which is F square that plus the other side which is equal magnitude. Also F square that minus two times one side times the other side so that there both F are squared times cosine 120 degrees. So the square root of two F squared minus two F squared times Cosine 120. I'm collecting these two together to make two F squared. And then factor out the two F squared. And that makes square root two times F times square root of one minus cos 120 and F is coulombs constant times one charge times the other charge divided by the distance between them squared and both these forces are the same because you know they're separated from the charges by the same distance and the charges are all equal magnitude so the forces is always going to be K Q squared over R squared. So we have square root two times K Q squared over R squared times square root one minus Cos 120 and that's square root Two times 8.988 times ten to the nine meter squared per coulombs squared times 17 micro coulombs which is times ten to the minus six columns squared divided by 15.0 centimeters which is time ten to the minus two meters squared times square root of one minus cos 120 and that's 199.958 Newtons which is about 2.00 times ten to the two Newtons and that's away from the center along the line connecting the center and the vertex. Or you could look at it a different way you could say the angle must be 30 degrees because since this is an isosceles triangle this is isosceles because two side links are the same that both F that means these two base angles have to be equal and we know this angle is a 120 and the and the all the angles in the Triangle added up make 180. So 180 minus 120 leaves 60 left over to be divided evenly between these two angles so 60 divided by two is 30 this angle here is 30 the resultant is then is 30 degrees below the positive x axis. When you're talking about the bottom right charge. And when you're talking about the bottom left charge it's the same picture except it's going to be directed 30 degrees below the negative x axis and this top charge and the x components of the force due to this charge in the force to this charge will be equal and opposite direction and will cancel. And so the only force is going to be direct straight up results and a straight up on the top force.