
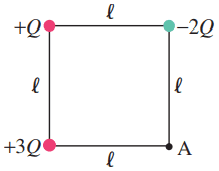
Three point charges are arranged at the corners of a square of side as shown in Fig. 17–39. What is the potential at the fourth corner (point A)?
In order to watch this solution you need to have a subscription.
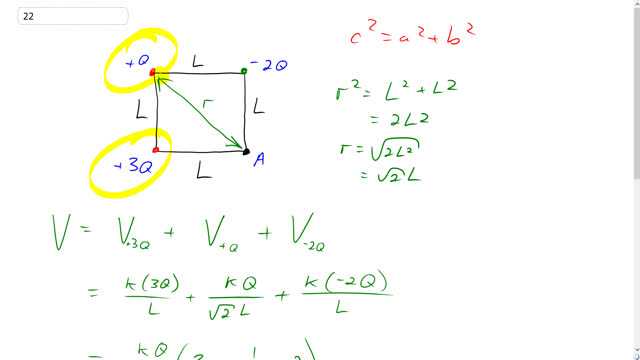
This is Giancoli Answers with Mr. Dychko So we need to find the potential at point A, and we have charges arranged in A square here where this one’s positive 3Q, this one’s positive 1Q, and this one’s negative 2Q. And, we get the resultant potential by just adding as scalars which means just adding as numbers all the potentials due to the each of these three charges and keeping in mind negative signs. So, potential is, in general, due to a point charge its k Q over r . So, we need to know the distance between each of these charges and this point A, off the charge negative 2Q, and positive 3Q. That's really straightforward, it’s the distance L the side length of the square. But for this charge on the diagonal opposite corner the distance is gonna be found by using Pythagoras', which is r squared is L squared, plus L squared, which is 2L squared, and then take the square root of both sides and you get r is square root of 2L squared, which is square root of two times L. So with that in mind, we can plug into this formula down here which says that the total voltage at point A is gonna be the voltage due to the positive 3Q charge, plus the voltage due to the positive Q charge, plus the voltage due to the negative 2Q charge and then were substituting into this formula for each of these terms here. And we have k times 3Q divided by L, potential due to the positive 3Q charge, and the plus k Q over root 2L, that’s where we use this distance r between the positive Q charge, and A and then plus k times negative 2Q divided by L. And you can factor out k Q over L and you get three plus one over root two, minus two. And well, three minus two is one, over root two there. And then multiply this by root two over root two to get two as the denominator. ‘Cause, I mean, you could leave it like this, but technically, it’s not simplified if you have a square root in the denominator. So let’s get rid of that by multiplying this by square root two over square root two, this makes root two over two, and then with a common denominator, we can add these two things. So well multiply this one by two over two, and so it has a common denominator, two, which we can then factor out and end up with k Q over 2L times two plus root two. And if it was me, I think this is totally fine, I mean enough, but this is technically a little better.
Why do we do scalar addition and not vector addition here? Is it because when we think of potential, we think of a magnitude of available potential occurring as a sort of pool versus, for example, in electric fields, which have an amount and direction its pushing or pulling a charge with a strength?
Well, scalar addition is used here because we're adding potential energies, and potential energy doesn't have direction. I think it might be helpful to consider what "potential" is, in order to make sense of the fact that it's a scalar. The first thing I always like to remind myself of is that when you hear of "potential", it actually is a lazy way of shortening the more complete term, which is "potential difference". Potential difference is the only thing that can ever be measured. With that said, the next obvious question is "difference" compared to what? In the case of a circuit with a battery, the potential difference is between the positive and negative terminals of the battery. In this question with point charges, the difference is between a point infinitely far away, and the given location of the charge. In other words we have a formula that tells us the amount of work an external force (like a hand pushing) would need to do in order to move the charge from infinitely far away to it's given location, which requires work since there's a force of repulsion as a result of (assuming the charges are of the same sign). When there are more charges in addition to , as there are on the other two corners of the square in this question, we use the formula a total of 3 times and add the results to find the total. The addition is as scalars since we're adding energies, which don't have direction.
Hope that helps!