
An electron starts from rest 24.5 cm from a fixed point charge Q = -6.50 nC. with How fast will the electron be moving when it is very far away?
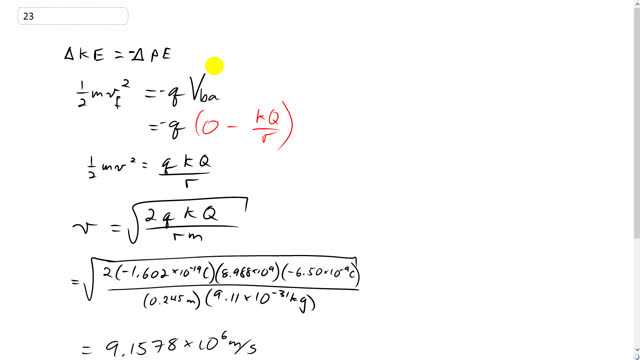
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The change in kinetic energy of this electron will be the opposite of its change in potential energy. So the change in its potential energy will be: the electron's charge, times the potential difference between its final position, really far away, and its initial position. And, so the potential really far away, its final potential, will be zero. And, that's minus the initial potential, which is k times capital Q over r, the potential resulting from this charge that's negative 6.5 nanocoulombs. So, these, this negative out here and this negative in here these two negatives makes a positive. So it's positive k q Q over r. And that equals one-half mv f squared, cause it starts from rest, so there's no one-half m v initial squared, this term is zero, so I didn't bother writing it. And, here we are with this line and we have to do some algebra to solve for v. And, we multiply both sides by two, and divide by m, and then square root both sides. So the final speed will be: square root of two, times the product of the charges, times Coulomb's constant, divided by the initial distance that the charge started at, the electron started at, and also divided by the electron mass. So that's square root of two, times negative 1.602 times 10 to the minus 19 Coulombs, times Coulomb's constant, times the charge that is starting near negative 6.5 times 10 to the minus 9 Coulombs, divided by its initial position of point 245 meters from this charge, and then times by the mass of electron, 9.11 times 10 to the minus 31 kilograms. And that gives a speed of 9.16 times 10 to the six meters pers second when it's really far away.
sick brah!!!!