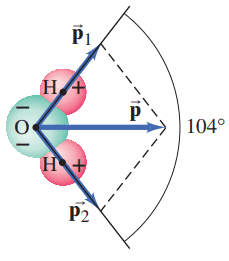
The dipole moment, considered as a vector, points from the negative to the positive charge. The water molecule, Fig. 17–42, has a dipole moment $\vec{p}$ which can be considered as the vector sum of the two dipole moments, $\vec{p}_1$ and $\vec{p}_2$, as shown. The distance between each H and the O is about $0.96 \times 10^{-10} \textrm{ m}$. The lines joining the center of the O atom with each H atom make an angle of $104 ^\circ$, as shown, and the net dipole moment has been measured to be $p = 6.1 \times 10^{-30} \textrm{ C}\cdot\textrm{m}$. Determine the charge q on each H atom.

VIDEO TRANSCRIPT

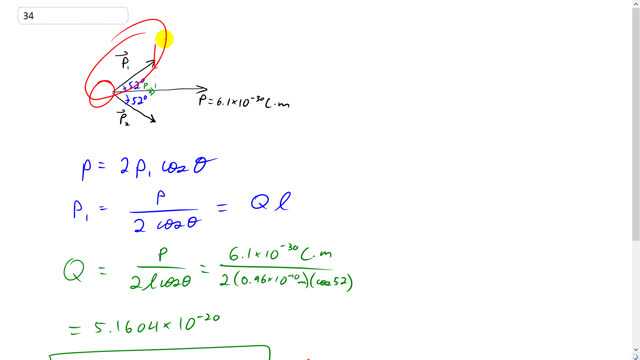
This is Giancoli Answers with Mr. Dychko. Here's the resultant dipole vector for this water molecule and it's the resultant of this vector connecting the oxygen to the hydrogen here. We call that P one dipole moment one and also added to this dipole moment here, P two connecting the oxygen to the other hydrogen. Oxygen hydrogen, hydrogen here. Because these are of equal magnitude, this resultant is going to bisect the angle between these vectors and we're told that that angle is a 104 degrees and so a 104 degrees divided by two because this resultant is going to be a bisector equals 52 degrees and so 52 degrees is the angle between the resultant and one of the dipole moments and the component of each dipole moment is going to be equal. And so the resultant is going to be two times the x component of one dipole moment. So we have P one times Cos theta gives us P one x, this adjacent leg of this triangle here. And times it by two since these dipole moments are going to be of equal magnitude and ends up being solved for one of the dipole moments by dividing both sides by two times Cos theta. And so we have P one is the dipole moment of resultant divided by two cos theta and this is Q l, that's the size of the dipole moment for one of these dipoles and will solve for Q by dividing this by l and dividing this by l as well. And so we have the charge on each end of one of these dipoles is P over two l Cos theta. And that's gonna be 6.1 times ten to the minus 30 coulomb meters is the net or resultant dipole divided by two times the distance between the oxygen and hydrogen which is 0.96 times ten to the minus 10 meters times Cos 52 and this gives 5.2 times ten to the minus 20 coulombs as the charge on each hydrogen atom. And we expected that to be less than the elementary charge of 1.6 times ten to the minus 19. Because this dipole is a result of unequal sharing of this one electron that the hydrogen has. But the hydrogen will get the electron sometimes and so there's not going to be… it's not completely transferred over to the oxygen and so the the hydrogen... if the electron was completely transferred over to the oxygen then the hydrogen would have a charge of one proton it would be a completely bare exposed proton and so it's charged would be 1.6 times ten to the 19, minus 19 coulombs. But we know that this is just unequal sharing so sometimes the hydrogen gets the electron and so the proton is somewhat obscured by the electron sometimes. And so we expected this charge to be less than the elementary charge.