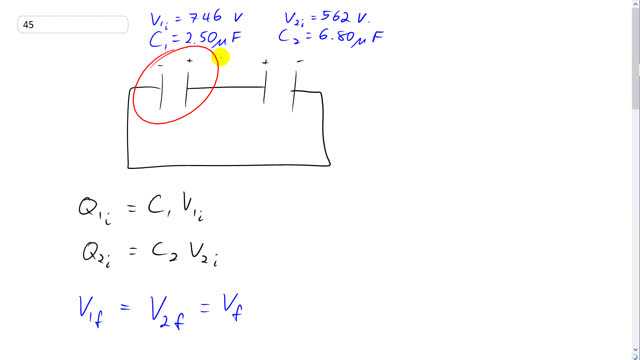
A $2.50$-$\mu \textrm{F}$ capacitor is charged to 746 V and a $6.80$-$\mu \textrm{F}$ capacitor is charged to 562 V. These capacitors are then disconnected from their batteries. Next the positive plates are connected to each other and the negative plates are connected to each other. What will be the potential difference across each and the charge on each? [Hint: Charge is conserved.]

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. V Initially before these capacitors are connected this way. This capacitor one will be charged to a voltage of 746 volts and we know its capacitance is two-and-a-half microfarads and this capacitor two will be charged to a voltage of 562 volts and it has a capacitance of 6.8 microfarads and then they are connected as shown in this picture with their two positive terminal terminals connected by a conductor and the negative terminals connected by a conductor. Now initially before they're connected the charge on capacitor one will be its capacitance times its voltage and the amount of charge on capacitor two on each plate will be its capacitor capacitance C Two times its initial voltage V Two i. Now after they're connected the voltage across each capacitor will be the same. And the reason for that is that you know at the very instant when this positive plate is connected to this positive plate. There will be a difference in potential and so some charge will move from one plate to the other but after that initial instant, it will equal out so that there's no charge will flow. It'll eventually balance itself out to the point where there's no voltage left between these two points and likewise with these negative plates charges will distribute during a very short instant when they're first connected but then eventually it'll even out so that there is some final voltage and that'll be the same between these two points as it is between these two points because this point and this point are equivalent. They have the same potential because they're connected by a conductor and this point and this point are also equivalent potentials because they are also connected by a conductor and so the potential difference between these two points will be the same as the potential difference between these two points. So V one final is going to equal V Two final and there's no need to distinguish them with a one divided by two. So let's just call it V final . Now the initial amount of charge on capacitor one plus the initial amount of charge in capacitor two is going to equal the final amount of charge on capacitor one plus the final amount of charge in capacitor two. It says that the total initial charge equals the total final charge because it was no positives and negatives being connected to neutralize any charges. The charges are just moving when you have these capacitors connected like this charges move between them. But the total amount of charge will not change. So then we substitute for the Q using these capacitance times voltage formulas. So Q one i is C one times V one i and Q two i is C one times V two i and Q one final is C one times V final and Q two final is C two times V final and the V final can be factored out from these two terms and leaving us with V final times C one plus C two . I can write that down I guess. We have V final times C one plus C two and then we divide this by the bracket and this by the bracket and leaving us with this line here. So V final is C one V one initial plus C two V two initial over the sum of the capacitances. So that's two and a half times ten to the minus six farads times 746 volts initial voltage across the capacitor one plus 6.8 times ten to the minus six farads times 562 volts divided by two and a half microfarads plus 6.8 micro farads and that gives 611 volts will be the final voltage across each capacitor. And the amount of charge on capacitor one will be its capacitance times its final voltage. And so that's going to be a two and a half times ten to the minus six farads time 611.46 volts which will give 1.53 times ten to the negative three coulombs and the capacitor two has a higher capacitance. So we expect the same amount of voltage to give more charge and sure enough we have 4.16 times ten to the minus three coulombs of charge or across capacity two.