VIDEO TRANSCRIPT

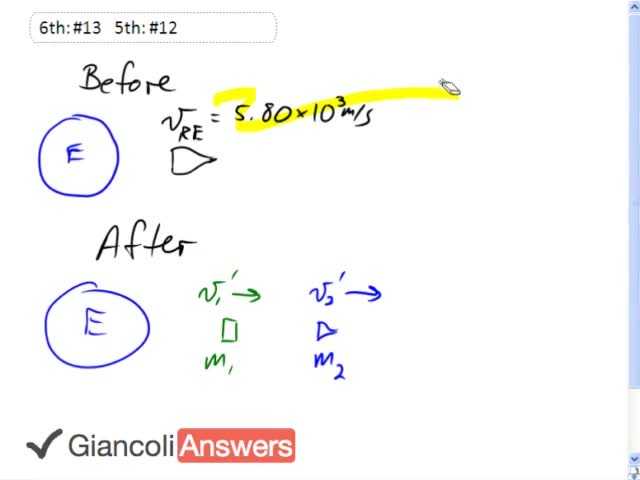
There’s a rocket moving away from the earth with a speed of five point eight times ten raised to power three meters per second and then there’s an explosion which separates the rocket into two equal pieces: ‘m1’ equals ‘m2’, that’s the mass of the two rocket fragments, let’s just call it ‘m’. The piece one has some speed ‘v1`’ which presumably is going to the right, we don’t exactly know that but let’s just suppose that that’s true for now and ‘v2`’ is definitely is got to be going to the right. So we are going to use conservation of momentum in order to answer this question and we are going to say that initially we have the rocket’s mass is two times ‘m’, ‘m’ being the mass of one fragment or one half of it. So initially we have two ‘m’ times the rocket’s speed, that is its velocity of the rocket with respect to the earth, and this equals the total final momentum: ‘m’ times the velocity of the first segment after the explosion, that’s prime means after the explosion plus ‘m’ times ‘v2`’, and these velocities are both with respect to the earth. So this ‘v1`’ and ‘v2`’, they make it a little bit problematic because they tell us what is the relative velocity of one piece with respect to the other instead of telling us the velocities with respect to the earth. So we’ll deal with that in just a second, first let’s observe that the ‘m’s all cancel away and this expression is: two ‘vRE’ equals ‘v1`’ plus ‘v2`’. They tell us the relative velocity of the two fragments that means the difference in their velocities. The velocity of segment two with respect to segment one is the difference in their velocities, so we can say that ‘v2`’ minus ‘v1`’ equals two point two times ten raised to power three meters per second. So you can make a substitution then into our momentum formula: ‘v2`’ is ‘v1`’ plus two point two times ten raised to power three, and then we’ll have an expression containing only ‘v1`’ which we can then solve. So we have, substituting ‘v2`’, we’ll say: two times ‘vRE’ equals ‘v1`’ plus ‘v1`’ plus two point two zero times ten raised to power three meters per second. Let’s solve for the ‘v1`’: two ‘v1`’ equals two ‘vRE’ minus two point two times ten raised to power three meters per second. So doing the arithmetic we get the ‘v1`’ is two times five point eight zero times ten raised to power three meters per second minus two point two times ten raised to power three meters per second minus two point two times ten raised to power three meters per second all divided by two giving us an answer of four point seven times ten raised to power three meters per second, that is ‘v1`’. And then ‘v2`’ is ‘v1`’ plus two point two times ten raised to power three, so that gives us six point nine times ten raised to power three meters per second. So ‘v2’ has sped up and ‘v1’ has slowed down which we expect if you imagine what would happen after this explosion ‘v2’ would be propelled faster away and ‘v1’ would still be going away but it would be going away more slowly than it was initially. So that’s part a done. Part b says how much kinetic energy does the explosion provide to the system and so it’s really asking what is the change in kinetic energy, Δ‘KE’, so that’s going to be the total final minus the total initial, so ‘KEf’ minus ‘KEi’. So we have one half mass times velocity of one of the segments squared, and it’s mass will be ‘m’ over two, ‘m’ is the mass of the whole rocket all put together, and this is times ‘v1`’ squared plus one half total rocket mass divided by two times ‘v2`’ squared and then we subtract away the kinetic energy we had to begin with, one half ‘m’ times the rocket’s initial velocity squared, and that is nine hundred and seventy five kilograms as the total rocket mass to begin with, before splitting up, over two times minus five point eight times ten raised to power three meters per second, and all that equals five point nine times ten raised to power eight Joules.