VIDEO TRANSCRIPT

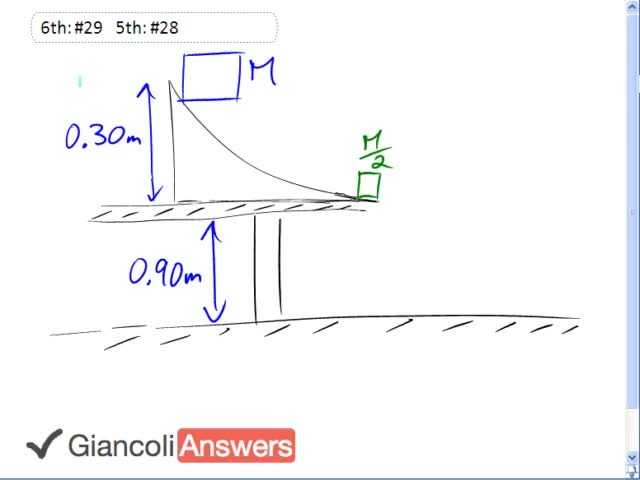
Our approach for this question is that we are first going to answer what is the speed of this big mass ‘M’ after it falls this height thirty centimeters. So when it gets to this point and is just about to impact the smaller green block what is the speed of the blue block going to be, and knowing that we’ll talk about conservation of momentum and figure out what the speeds of the two blocks will be after the collision occurs. So in other words, what is the launch speed that each of them is going to have sideways after the collision. Then we are going to use kinematics and figure out how long it will take to fall this height, how long does it take things to free fall due to the acceleration due to gravity a height of ninety centimeters. And then knowing that time, multiply it by this launch velocity which is entirely horizontal we’ll figure out how far away from the edge the blocks will land. So from conservation of energy we can say that the initial potential energy of the big blue block equals its final kinetic energy, it has no initial kinetic energy and it has no final potential energy. So that is: it’s mass ‘M’ times ‘g’ times ‘h’ equals one half its mass times its final velocity squared. So its final velocity will be: the square root of two times ‘g’ times ‘h’ because we multiply both sides by two here and cancel out the ‘M’s and square root it. So its final velocity is the square root of two times nine point eight times zero point three meters, and that is two point four two four nine meters per second. We are keeping lots of digits because this is an intermediate calculation. So now we know what the speed of this block will be when it gets to this point and it’s just about to impact the smaller block. Now use momentum: the initial total momentum which is just contained in block one because block two is initially at rest equals the total final momentum which is ‘M’ times ‘v1`’ plus the mass of the second block which is ‘M’ over two times ‘v2’ times ‘v2`’. And using conservation of energy because we are told this collision is elastic: ‘v1’ equals ‘v2`’ minus ‘v1`’. Normally I would have said, ‘v1’ minus ‘v2’ here but ‘v2’ is initially zero. So we’ll solve the second equation for ‘v2`’ and then substitute that to be able to determine what ‘v1`’ is. So we have: ‘v2`’ equals ‘v1’ plus ‘v1`’. So we’ll substitute that here. We have ‘M’ times ‘v1’ equals ‘M’ times ‘v1`’ plus ‘M’ over two times ‘v1’ plus ‘v1`’. Let’s multiply everything by two to get rid of that denominator and so we have: two times ‘M’ times ‘v1’ equals two times ‘M’ times ‘v1`’ plus ‘M’ times ‘v1’ plus ‘M’ times ‘v1`’. Let’s also cancel out the ‘M’s because that is a common factor, so that’s: two times ‘v1’ equals two times ‘v1`’ plus ‘v1’ plus ‘v1`’. To solve for ‘v1`’ we simplify to get: three times ‘v1`’ equals ‘v1’, so the speed of the initial big block is going to be one third what it was after the collision, so ‘v1`’ is going to be two point four two four nine meters per second divided by three. So after the collision it will slow down to zero point eight zero eight two nine meters per second. The speed of the little block which is initially at rest of ‘v2`’ and it was ‘v1’ plus ‘v1`’ that’s what we said from this conservation of energy expression is going to be two point four two four nine meters per second plus zero point eight zero eight two nine and that makes three point two three three two meters per second. So now we have both of the launch velocities, we have to turn to kinematics now to figure out what time it takes for the blocks to fall. And then knowing that time multiplied by these launch velocities which are entirely horizontal and figure out how far the blocks would go before they hit the ground. We’re going to use the equation: ‘d’ equals one half ‘a’ times ‘t’ squared. So this distance it’s going to fall, the question we are answering is how long will it take to fall? So we’ll solve for ‘t’ and ‘t’ is going to be: the square root of two times ‘d’ divided by ‘g’. So ‘t’ is: the square root of two times zero point nine zero meters over nine point eight meters per second squared and that equals zero point four two eight five seven seconds. So after the collision we’ll have large block here with mass ‘M’, and that will be a distance ‘d1’ from the edge of the table and we’ll have the little block over here some distance ‘d2’ from the edge of the table. So ‘d1’ is” ‘v1`’ multiplied by ‘t’, so that’s zero point eight zero eight two nine meters per second times zero point four two eight five seven seconds and we get our answer zero point three five meters, that’s how far the large block will go. The small block: ‘v2`’ multiplied by ‘t’ is going to be three point two three three two meters per second times zero point four two eight five seven seconds and that equals one point four meters for the small block.