VIDEO TRANSCRIPT

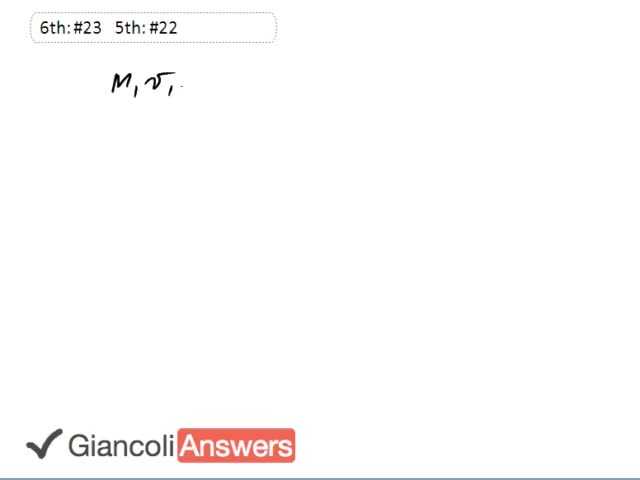
We’ll start this question by writing down conservation of momentum. So that is to say ‘m1’ times ‘v1’ plus ‘m2’ times ‘v2’ equals ‘m1’ times ‘v1`’ plus ‘m2’ times ‘v2`’. We know that the initial velocity of the puck number two is zero and so ‘m2’ times ‘v2’ disappears. And we’ll call this equation one. Equation two will be our conservation of energy equation since we’re told the collision is elastic. So: ‘v1’ minus ‘v2’ is ‘v2`’ minus ‘v1`’ and this term is also zero. And we’ll rearrange number two and solve for ‘v2`’ and then we’ll substitute that into equation one so that we have only one unknown variable in that equation. So ‘v2`’ equals ‘v1’ plus ‘v1`’ and we’ll substitute this in equation one so equation one becomes: ‘m1’ times ‘v1’ equals ‘m1’ times ‘v1`’ plus ‘m2’ times ‘v1’ plus ‘v1`’. Now we’ll solve for ‘v1`’: ‘m1’ times ‘v1’ is ‘m1’ times ‘v1`’ plus ‘m2’ times ‘v2`’. So we have ‘v1`’ factored out from ‘m1’ plus ‘m2’ and that equals ‘m1’ times ‘v1’ minus ‘m2’ times ‘v1’ giving us the ‘v1`’ is ‘v1’ times ‘m1’ minus ‘m2’ ‘m1’ plus ‘m2’. Substituting in numbers we have three point zero zero meters per second as the incoming velocity of the puck, we’ll call it positive, we’ll say East is positive direction, times zero point four five zero kilograms minus zero point nine zero zero kilograms and see that this difference will be negative which means that the puck will rebound, it will be going backwards after this coalition since it’s mass is less than the stationery puck and this equals negative one point zero zero meters per second. So the first incoming puck, puck number one, will be going backwards after the collision. Puck two after the collision is ‘v1’ plus ‘v1`’ so that’s three point zero meters per second minus one point zero and this gives two meters per second, which is positive so the pack number two will be going to the right or in east direction. If we wanted to draw a picture, we’d have puck number two here after the collision going at two meters per second and puck number one after the collision is going one meter per second west.