VIDEO TRANSCRIPT

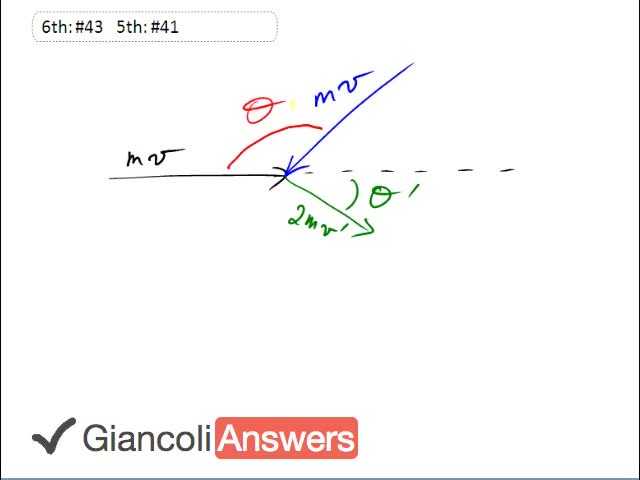
So we have two objects here that are going to collide here and they have the same mass, and the same incoming velocity and they’re separated by some angle ‘θ’ that we need to find. After the collision they stick together because its completely inelastic and they have some speed ‘v`’ which we’re actually told is ‘v’ divided by three and there’ll be some angle here as well, ‘θ`’, with respect to the initial velocity of one of the incoming objects. So our job is to find ‘θ’ and we’ll start the usual way for these questions by writing down the X and why components of momentum: so in the X direction we have ‘mv’ plus ‘m’ times ‘v’ cosine ‘θ’, that’s the component of this incoming object’s momentum in the X direction, and that equals two ‘m’ times ‘v`’ cosine ’θ`’. We have a two ‘m’ here because the objects stick together and one of them is mass ‘m’ and the other is mass ‘m’ as well, so we have total mass two ‘m’. In the Y direction we have: ‘m’ times ‘v’ sine ‘θ’ equals two ‘m’ times ‘v`’ sine ‘θ’`. So the Y component of this object’s momentum equals the Y component of the total momentum after the collision. Equation 1b we’ll write as: ‘v’ plus ‘v’ cosine ‘θ’ equals two times ‘v’ over three, which is one plus cosine ‘θ’ equals two thirds cos ’θ`’. And equation 2b we have ‘v’ sine ’θ`’ equals two times ‘v’ over three, we’re substituting for ‘v`’, which then is: sine ‘θ’ equals two thirds sine ’θ`’. We’re going to use the Pythagorean identity for trigonometry: sine squared plus cosine squared equals one, and we’ll square equation 1b and we’ll also square equation 2b then add them then we’ll see that we have two thirds cosine squared ’θ`’ plus two thirds sine squared ’θ`’ and so we can get rid of those and just substitute with the number one and we’ll have gotten rid of ’θ`’ that way, so: we have one plus two times cosine ‘θ’ plus cosine squared θ, what I just did is that I squared this binomial, plus sine squared θ, equals four ninths cosine squared ’θ`’ plus four ninths sine squared ’θ`’, which is four ninths times cosine squared ’θ`’ plus sine squared ’θ`’ and this equals four ninths. So we have one plus two cosine ‘θ’ plus one equals four ninths, two cosine ‘θ’ equals four ninths minus two, two cosine ‘θ’ equals four ninths minus eighteen ninths which is negative fourteen ninths, so cosine ‘θ’ is negative fourteen eighteenths and that gives us θ as one hundred and fourty one degrees when we take the inverse cosine of negative fourteen eighteenths. And that’s our answer.