VIDEO TRANSCRIPT

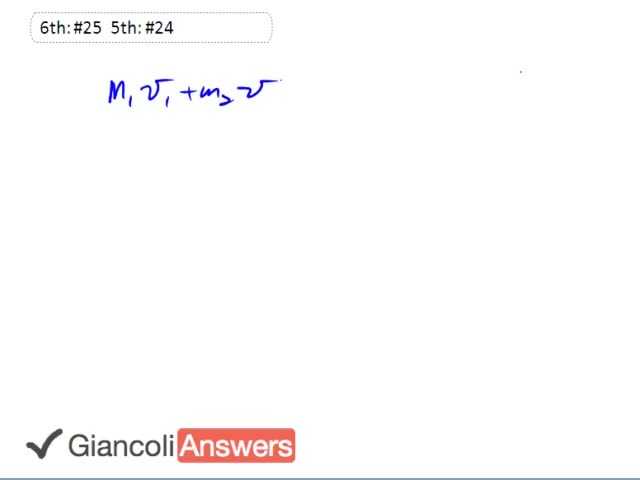
Let’s begin by writing down conservation of momentum. ‘m1’ times ‘v1’ plus ‘m2’ times ‘v2’ equals ‘m1’ times ‘v1`’ plus ‘m2 times ‘v2`’, and we’ll call that equation one. Equation two will come from conservation of energy because we’re told the collision is elastic, so that’s ‘v1’ minus ‘v2’ equals ‘v2`’ minus ‘v1`’. We’ll rearrange equation two and solve for one of the unknowns so that we can substitute into equation one, and we have: ‘v2`’ equals ‘v1’ minus ‘v2’ plus ‘v1`’. We’ll make that substitution into equation one for ‘v2`’ so equation one becomes: ‘m1’ times ‘v1’ plus ‘m2’ times ‘v2’ equals ‘ m1’ times ‘v1`’ plus ‘m2’ times ‘v1’ minus ‘v2’ plus ‘v1`’, which is ‘m1’ times ‘v1’ plus ‘m2’ times ‘v2’ equals ‘m1’ times ‘v1`’ plus ‘m2’ times ‘ v1’ minus ‘m2’ times ‘v2’ plus ‘m2’ times ‘v1`’. We’ll collect the ‘v1`’ terms on the left because that’s what we’re trying to solve for here and we get ‘v1`’ factored out from ‘m1’ plus ‘m2’ equals ‘m1’ times ‘v1’ plus ‘m2’ times ‘v2’ minus ‘m2’ times ‘v1’ plus ‘m2’ times ‘v2’ so in the end we get: ‘v1`’ is ‘m1’ times ‘v1’ plus two times ‘m2’ times ‘v2’ minus ‘m2’ times ‘v1’ all divided by ‘m1’ plus ‘m2’. We’ll just substitute some numbers in there and get our answer: zero point zero six kilograms is the mass of the incoming ball times initial velocity of two point five zero meters per second plus two times the mass of the second ball. Now the velocity of the second ball leaves some room for interpretation; it tells us the ball is moving away at one point one five meters per second, I’m going to assume that that’s the speed with respect to the ground, that makes the most sense. it could be interpreted as being the speed with which it’s receding from the incoming ball but then the balls would never collide so that wouldn’t make sense that way. And so we’re going to divide all this by the sum of the masses, zero point six kilograms plus zero point nine kilograms and we’ll get our answer of zero point eight eight meters per second; so the incoming ball will be on the same direction but it’ll slow to zero point eight eight meters per second. The second ball is going to speed up though and it’s velocity after the collision is ‘v1’ minus ‘v2’ plus ‘v1`’, so that’s two and half meters per second minus one point one five plus zero point eight eight and that gives us two point two meters per second. For the 5th Edition there’s some slightly different numbers, the velocity is one point zero zero meters per second, that’s the initial speed of the second ball. And the answer for ‘v1`’ then is going to instead be zero point seven zero meters per second for the 5th Edition and substituting, the 5th edition answer is the same though, two point two meters per second.