VIDEO TRANSCRIPT

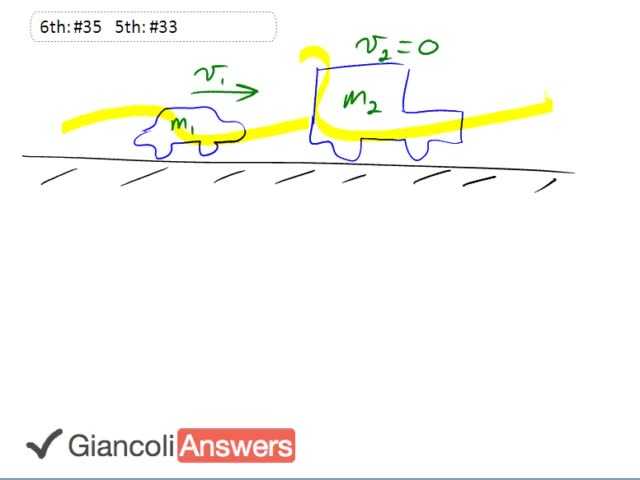
So this smaller vehicle here is going to impact a larger vehicle which is initially at rest at a red light and we know what the acceleration is going to be because we know friction. We also know how far the combined wreck goes and so from that we can figure out the initial speed of this wreck and then knowing that we’ll be able to use momentum to figure out what must have been the speed of the incoming car. So we’ll talk about momentum first of all. So we have that 'm1’ times 'v1’ equals 'm1’ plus 'm2’ times 'v`’, so the total initial momentum which is just of the car equals the combined mass when it becomes a wreck times their combined velocity. And we can solve that for 'v1’: that’s 'm1’ plus 'm2’ over 'm1’ times 'v`’. We know that the force of friction in this case is the net force when the two are sliding after the collision they’re sliding coming to a stop, there is only one force acting on them which is friction. So that means that ‘µ’ times ‘FN’ which is a friction formula equals ‘m’ times ‘a’ which is the net force formula and ‘FN’ in this case is ‘m’ times ‘g’, it’s the force of gravity, because they are not accelerating vertically. So we have ‘µ’ times ‘m’ times ‘g’ equals ‘m’ times ‘a’ and the ‘m’s cancel meaning that ‘a’ equals ‘µ’ times ‘g’. So now we know the deceleration of the wreck we’ll use the kinematics formula 'vf’ squared equals 'v1’ squared plus two times ‘a’ times ‘d’ because we know all these things except for 'vi’ which is what we want to find. We know that they come to a stop, we know what the acceleration is and we know how far they go because the question tells us. So we’ll solve for 'vi’: 'vi’ is the square root of two times ‘a’ times ‘d’ which is the square root negative two times ‘µ’ times ‘g’ times the distance that it slides, then substitute for 'vi’ with 'v`’, the 'vi’ is the speed just when the wreck begins and that’s 'v`’ so far as the momentum is concerned. So 'v`’ is the speed after the two cars collide and 'vi’ here is the same speed as that speed that the wreck starts to slide at. So we have: 'v1’ is 'm1’ plus 'm2’ over 'm1’ times this expression square root of two times ‘µ’ times ‘g’ times ‘d’. ‘g’ or the acceleration is negative and so this ‘µ’ times ‘g’ should be a negative expression so the negative sign disappears, so we have nine hundred and twenty kilograms plus two thousand three hundred kilograms divided by nine hundred and twenty times square root of two times zero point eight, the coefficient of friction, times nine point eight which is ‘g’ times two point eight meters that the wreck slides. And this gives twenty three meters per second. Now for the 5th Edition the masses are slightly different, we have one thousand kilograms is the incoming vehicle and it impacts a vehicle which is initially at rest of mass two thousand two hundred kilograms and the coefficient of friction is instead zero point four so for the 5th Edition the car must have initially going fifteen meters per second.