VIDEO TRANSCRIPT

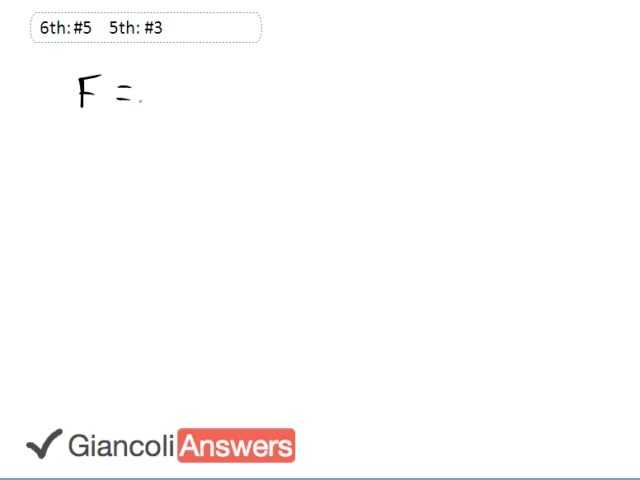
We’ll find the force on the rocket due to the expelled gases by saying ‘F’ is to change in momentum over change in time and so we’ll have to find this change in momentum. We can define the amount of time to be whatever we want, we can consider one second for convenience, and in that time what mass of gas will be expelled? The mass of gas will be: one thousand five hundred kilograms every second times one second and so this will give us the amount of gas expelled which is one thousand five hundred kilograms. So: ‘F’ is equal to ‘m’ times ‘v1`’ minus ‘m’ times ‘v’. So what we’ve established so far is what ‘m’ and‘t’ are, one thousand five hundred and one, what about ‘v1`’ and ‘v’? ‘v1`’ is given to us, it’s the speed that the gas is zipping out f the gas, and ‘v’ is zero, the gas is initially at rest, initially liquid fuel inside the engine which is not moving. Then the fuel explodes so it starts from rest and then is exhausted out of the back of the rocket. So: ‘F’ is one thousand five hundred kilograms, the mass of gas expelled in one second, times its speed of four point zero times ten raised to power four meters per second divided by one second giving us an answer of six point zero times ten raised to power seven newtons as the force on the rocket. In the 5th Edition the rocket weighs one thousand three hundred kilograms instead so the answer would be five point two times ten raised to the power seven newtons. Notice that the rocket works out in space due to the conservation of momentum and does not require any surface to shoot the gas off of so it’s a misconception to think that the gas needs to push against the ground in order to lift the rocket up, that’s not true. It’s a conservation of momentum phenomenon that’s responsibly for this rocket being propelled by the gas, the gas goes one way and the rocket goes the other in order to conserve momentum.