GiancoliAnswers

You are here

  4. Problem 19
Select a problem

a) $p_{fb_i}=380 kg \cdot m/s$
b) $\Delta p_{fb} = -380 kg \cdot m/s$
c) $\Delta p_t = 380 kg \cdot m/s$
d) $F_t = 5.1 \times 10^2 N$

Giancoli 6th Edition, Chapter 7, Problem 19

(3:11)

Chapter 7, Problem 19 is solved.

View sample solution

Transcript for this Giancoli solution

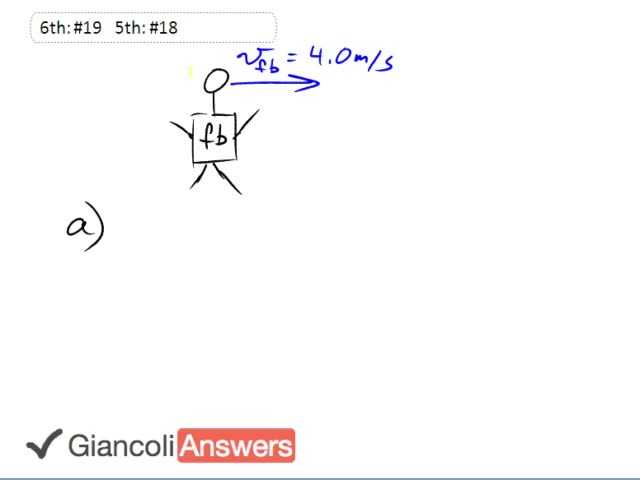
Let’s define the eastern direction as positive in which case the fullback has a positive velocity of four meters per second. Now the fullback’s initial momentum ‘Pfbi’ initial is mass times velocity, that’s ninety five kilograms times four point zero meters per second and that means his initial momentum is three hundred and eighty kilograms meters per second. In part b we want to know the impulse experience by the fullback, that is the change in momentum of the fullback, so that’s the fullbacks final momentum minus the initial momentum which is going to be negative three hundred and eighty kilograms meters per second because the final momentum of the fullback is zero so we just have the negative of the initial momentum which we calculated in part a. In part c we want to know the change in momentum of the tackler and they are moving in the opposite direction, they are running west, and their change in momentum is going to be the negative change in momentum of the fullback, so that’s negative negative three hundred and eighty kilograms meters per second, so that’s positive three hundred and eighty kilograms meters per second is the impulse experienced by the tackler. The force on the tackler is the change in momentum of the tackler divided by time which is three hundred and eighty kilograms meters per second divided by zero point seven five seconds which is five point one times ten raised to power two newtons. In the 5th Edition the only change is the mass of the fullback, and that’s a hundred and fifteen kilograms. So the answer changes for the 5th Edition to four point six times ten raised to power two kilogram meters per second. And that carries to the rest of the answers here too, and the force then in the 5th Edition is six point one times ten to the power two newtons.