VIDEO TRANSCRIPT

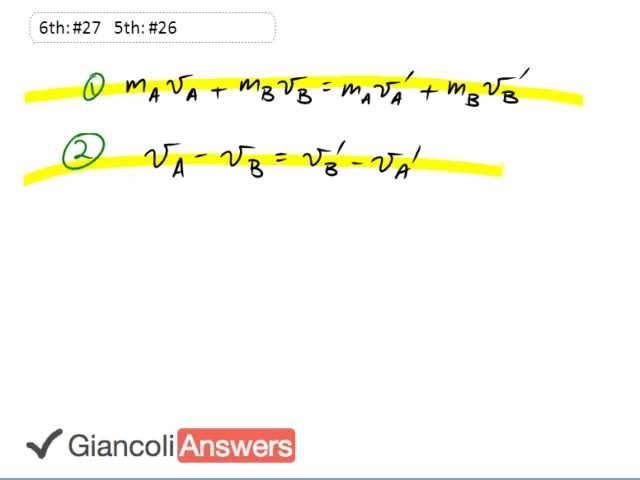
We have our conservation of momentum equation, equation one and we have the conservation of energy equation since it’s an elastic collision. We’ll solve for ‘vb`’ from equation two and substitute into equation one so that we have only one unknown in equation one. So equation two after we do a bit of work after we do a bit of work on it, we’ll call it equation 2b, is: ‘vb`’ equals ‘va’ minus ‘vb’ plus ‘va`’ and we’ll substitute for that in equation one. So equation one becomes: ‘ma’ times ‘va’ plus ‘mb’ times ‘vb’ equals ‘ma’ times ‘va`’ plus ‘mb’ times ‘va’ minus ‘vb’ plus va`’, then we’ll expand the bracket and collect the ‘va`’ terms in the left but let’s just expand first. Let’s have a minus here. So it’s minus ‘mb’ times ‘vb’ plus ‘mb’ times ‘va`’. So we have ‘va`` times ‘ma’ plus ‘mb’ equals ‘ma’ times ‘va’ minus ‘mb’ times ‘va’ which is plus two ‘mb’ times ‘vb’. Now let’s divide both sides by ’ma’ plus ‘mb’ and we’ll have solved our ‘va`’: ‘ma’ times ‘va’ minus ‘mb’ times ‘va’ plus two ‘mb’ times ‘vb’ divided by ‘ma’ plus ‘mb’. So we have mass a is four hundred and fifty kilograms times its initial velocity of four point five meters per second minus five hundred and fifty kilograms for the mass of the second guy times the initial velocity of car a plus two times mass of the second car times its initial velocity of three point seven then we’ll divide all that by the sum of the masses, four hundred and fifty kilograms plus five hundred and fifty kilograms. This equals three point six two meters per second. So that’s around say for what the velocity of car a will be after the collision. Now car b we know is going to have the velocity ‘va’ minus ‘vb’ plus ‘va`’ and so this is four point five zero minus three point seven meters per second plus three point six two meters per second and that gives four point four two meters per second as the velocity of car b after the collision. So it speeds up because it gets rear ended from behind. In part b we’re asked what the change of momentum is for the two cars. So ‘ΔP’ for car a is car a’s final momentum minus its initial momentum. So it’s going to be ‘ma’ times ‘vf’ for car a minus mass a times ‘vi’ for car a, which is ‘ma’ times ‘vfa’ minus ‘via’ and now we can put in some numbers there. So we have the change in momentum for car a is four hundred and fifty kilograms times three point six two meters per second minus four point five zero meters per second, and this is going to be negative which is no surprise since the car slows down, so we have negative three hundred and ninety six kilogram meters per second. That’s the impulse of car a. It loses some momentum that’s why it’s negative, it’s negative because the change of momentum is directed in the negative direction which indeed slows it down since its momentum was initially in the positive direction; and the momentum continues to be in the positive direction just less of it. And for car b: ‘mb’ times ‘vfb’ minus ‘vib’ same expression as for car a and that’s going to end up being five hundred and fifty kilograms times four point four two meters per second minus three point seven meters per second and we end up with positive three hundred and six kilogram meters per second. Now this turns out to be the negative of the change of momentum for car a which is no surprise because it’s a closed system and it’s a Newton’s third law sort of thing where the change in momentum of one object is equal but opposite to the change of momentum of the next object.